题目内容
(本小题满分14分)设数列 的前
的前 项和为
项和为 ,
, ,且对任意正整数
,且对任意正整数 ,点
,点 在直线
在直线 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1) 的通项公式为
的通项公式为 ;
;
(2)数列 的前
的前 项和为
项和为 .
.
【解析】
试题分析:(1) 点
点 在直线
在直线 上
上

 1分
1分
当 时,
时, 2分
2分
两式相减得:
即

 3分
3分
又当 时,
时,
 4分
4分

 是首项
是首项 ,公比
,公比 的等比数列 5分
的等比数列 5分

 的通项公式为
的通项公式为 6分
6分
(2)由(1)知, 7分
7分
 8分
8分
 9分
9分
两式相减得: 11分
11分
 13分
13分
 数列
数列 的前
的前 项和为
项和为 14分
14分
考点:考查了等比数列的通项公式,利用错位相减法求和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
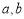 ,两个平面
,两个平面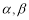 .给出下面四个命题:( )
.给出下面四个命题:( )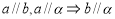 ;
; 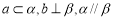
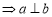 ;
;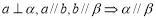 ;
; 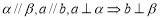 .
. 展开式中的常数项为________________(具体数字作答).
展开式中的常数项为________________(具体数字作答). ,向量
,向量 ,
, ,且
,且 ,则
,则 ( )
( ) B.
B. C.B.
C.B. D.
D.
 与
与 的方程分别为
的方程分别为 与
与 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,则曲线
轴的正半轴,建立平面直角坐标系,则曲线 与
与 交点的直角坐标为 .
交点的直角坐标为 . 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( )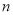 的值为
的值为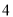 ,则输出
,则输出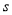 的值为____________.
的值为____________.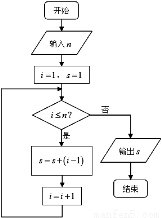
 ,B(5,1),则以线段AB为直径的圆的方程的一般式
,B(5,1),则以线段AB为直径的圆的方程的一般式