题目内容
在四棱锥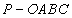 中,
中,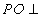 底面
底面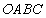 ,
,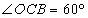 ,
,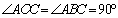 , 且
, 且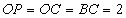 .
.
(1)若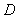 是
是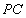 的中点,求证:
的中点,求证: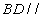 平面
平面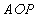 ;
;
(2)求二面角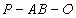 的余弦值.
的余弦值.
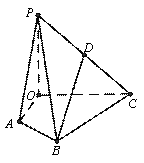
解:(1)如图,建立空间直角坐标系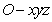 .连接
.连接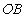 ,易知
,易知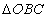 为等边三角形,
为等边三角形,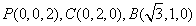 ,则
,则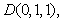
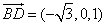 .又易知平面
.又易知平面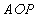 的法向量
的法向量
为 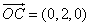 ,
,
由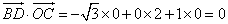 ,得
,得
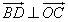 ,
,
所以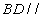 平面
平面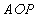 ………………………6分
………………………6分
(2)在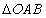 中,
中,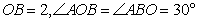 ,则
,则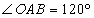 ,由正弦定理,
,由正弦定理,
得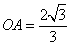 ,即
,即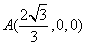 ,所以
,所以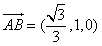 ,
,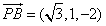 .
.
设平面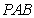 的法向量为
的法向量为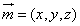 ,
,
由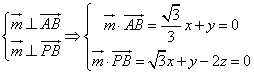 ,
,
令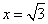 ,则
,则 ,即
,即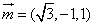 …………………10分
…………………10分
又平面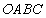 的法向量为
的法向量为 ,
,
所以,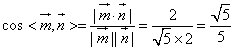 .
.
即二面角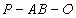 的余弦值为
的余弦值为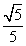 ………………………13分
………………………13分

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 的前
的前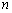 项和
项和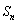 满足
满足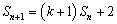 ,又
,又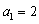 ,
,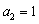 .
. ,且
,且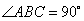 ,
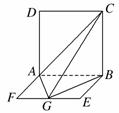
,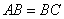 ,则B、C两点间的球面距离为
,则B、C两点间的球面距离为 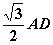 ,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
,G是EF的中点,则GB与平面AGC所成角的正弦值为( ) 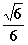 B.
B. 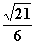 C.
C. 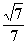 D.
D.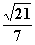
 和
和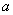 ,且长为
,且长为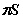 B.
B. 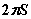 C.
C. 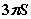 D.
D. 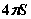
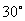 B.
B.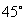 C.
C.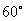 D.
D.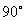
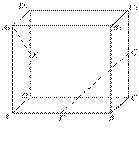
 的抛物线方程是 ( )
的抛物线方程是 ( ) B.
B.  C.
C.  D.
D. 
 的解集是 ( )
的解集是 ( ) B
B  C
C  D
D 