题目内容
 如图所示,B点坐标为(-c,0),C点坐标为(c,0),AH⊥BC,垂足为H,且
如图所示,B点坐标为(-c,0),C点坐标为(c,0),AH⊥BC,垂足为H,且. |
| BH |
. |
| HC |
(1)若
| AB |
| AC |
(2)
| AD |
| DB |
| 7 |
| 2 |
分析:(1)根据题意算出H(
,0),可设A(
,y0),得到向量
、
关于c、y0的坐标,由
?
=0列式化简得到
=
c2,由两点间的距离公式算出|AB|、|AC|关于c的式子,从而算出|AB|+|AC|=(
+1)c,由此利用椭圆离心率的公式,即可算出该椭圆的离心率;
(2)设D(x1,y1),根据向量的坐标运算公式算出x1=
,y1=
.将A、D两点的坐标代入椭圆方程,组成方程组并消去
得e2=
,根据-5≤λ≤
算出e2∈[
,
],从而解出
≤e≤
.
| c |
| 2 |
| c |
| 2 |
| AB |
| AC |
| AB |
| AC |
| y | 2 0 |
| 3 |
| 4 |
| 3 |
(2)设D(x1,y1),根据向量的坐标运算公式算出x1=
| ||
| 1+λ |
| y0 |
| 1+λ |
| y | 2 0 |
| λ+2 |
| λ-1 |
| 7 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
解答:解:(1)∵B(-c,0),C(c,0),
∴由
=3
,解出H(
,0),
∵AH⊥BC,可设A(
,y0),得
=(-c-
,-y0),
=(c-
,-y0)
∴由
?
=0,得(-c-
)(c-
)+y02=0,化简得
=
c2,
∴|AB|=
=
c,|AC|=
=c,
∴以B、C为焦点椭圆的长轴2a=|AB|+|AC|=(
+1)c,
可得e=
=
=
-1.
(2)设D(x1,y1),
∵
=λ
,A(
,y0),B(-c,0),∴x1=
,y1=
,
将A(
,y0),D(
,
)代入
+
=1,
可得
,消去
得e2=
,
∵-5≤λ≤-
,可得
≤
≤
,
∴e2∈[
,
],解之得
≤e≤
.
∴由
| BH |
| HC |
| c |
| 2 |
∵AH⊥BC,可设A(
| c |
| 2 |
| AB |
| c |
| 2 |
| AC |
| c |
| 2 |
∴由
| AB |
| AC |
| c |
| 2 |
| c |
| 2 |
| y | 2 0 |
| 3 |
| 4 |
∴|AB|=
(-c-
|
| 3 |
(
|
∴以B、C为焦点椭圆的长轴2a=|AB|+|AC|=(
| 3 |
可得e=
| c |
| a |
| 2 | ||
|
| 3 |
(2)设D(x1,y1),
∵
| AD |
| DB |
| c |
| 2 |
| ||
| 1+λ |
| y0 |
| 1+λ |
将A(
| c |
| 2 |
| ||
| 1+λ |
| y0 |
| 1+λ |
| x2 |
| a2 |
| y2 |
| b2 |
可得
|
| y | 2 0 |
| λ+2 |
| λ-1 |
∵-5≤λ≤-
| 7 |
| 2 |
| 1 |
| 3 |
| λ+2 |
| λ-1 |
| 1 |
| 2 |
∴e2∈[
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
点评:本题给出三角形满足的几何关系和向量等式,求椭圆的离心率取值范围.着重考查了向量的坐标运算、向量的数量积和椭圆的简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
 (2012•湖南)函数f(x)=sin (ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
(2012•湖南)函数f(x)=sin (ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
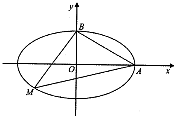 (2012•厦门模拟)某公园内有一椭圆形景观水池,经测量知,椭圆长轴长为20米,短轴长为16米.现以椭圆长轴所在直线为x轴,短轴所在直线为y轴,建立平面直角坐标系,如图所示.
(2012•厦门模拟)某公园内有一椭圆形景观水池,经测量知,椭圆长轴长为20米,短轴长为16米.现以椭圆长轴所在直线为x轴,短轴所在直线为y轴,建立平面直角坐标系,如图所示.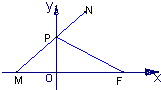 如图所示,设点F坐标为 (1,0 ),点P在y轴上运动,点M在x轴运动上,其中
如图所示,设点F坐标为 (1,0 ),点P在y轴上运动,点M在x轴运动上,其中