题目内容
(一、二级达标校做)
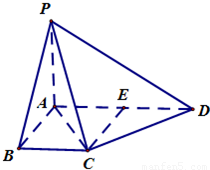
如图,在梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PA=
.
(Ⅰ) 证明:平面PAC⊥平面PCD;
(Ⅱ)若E为AD的中点,求证:CE∥平面PAB;
(Ⅲ)求四面体A-FCD的体积.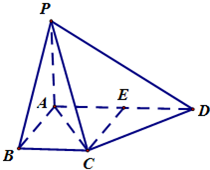
如图,在梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PA=
| 2 |
(Ⅰ) 证明:平面PAC⊥平面PCD;
(Ⅱ)若E为AD的中点,求证:CE∥平面PAB;
(Ⅲ)求四面体A-FCD的体积.

(I)∵PA⊥平面ABCD,CD?平面ABCD
∴PA⊥CD
又CD⊥PC,PA∩PC=P.
∴CD⊥平面PAC
∵CD?平面PCD
∴平面PAC⊥平面PCD.
(Ⅱ)∵AD∥BC,AB⊥BC,AB=BC=1,
∴∠BAC=45°,∠CAD=45°,AC=
∵CD⊥平面PAC,CA?平面PAC
∴CD⊥CA,
∴Rt△ACD中,AD=
AC=2
又∵E为AD的中点,
∴四边形ABCE是正方形,
∴CE∥AB
∵CE?平面PAB,AB?平面PAB
∴CE∥平面PAB.
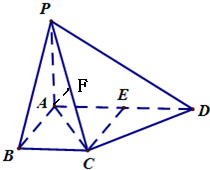
(Ⅲ)设PC的中点为F,连AF.
在Rt△PAC中,PA=
,AC=
,PC=2,
∴AF⊥PC,且AF=1,
由(Ⅰ)知:平面PAC⊥平面PCD,
∵平面PAC∩平面PCD=PC
∴AF⊥平面PCD,
在Rt△PCD中,CD=
,PC=2,
∴S△PCD=
CD•PC=
,
∴VA-PCD=
S△PCD•AF=
•
•1=
∴PA⊥CD
又CD⊥PC,PA∩PC=P.
∴CD⊥平面PAC
∵CD?平面PCD
∴平面PAC⊥平面PCD.
(Ⅱ)∵AD∥BC,AB⊥BC,AB=BC=1,
∴∠BAC=45°,∠CAD=45°,AC=
| 2 |
∵CD⊥平面PAC,CA?平面PAC
∴CD⊥CA,
∴Rt△ACD中,AD=
| 2 |

又∵E为AD的中点,
∴四边形ABCE是正方形,
∴CE∥AB
∵CE?平面PAB,AB?平面PAB
∴CE∥平面PAB.
(Ⅲ)设PC的中点为F,连AF.
在Rt△PAC中,PA=
| 2 |
| 2 |
∴AF⊥PC,且AF=1,
由(Ⅰ)知:平面PAC⊥平面PCD,
∵平面PAC∩平面PCD=PC
∴AF⊥平面PCD,
在Rt△PCD中,CD=
| 2 |
∴S△PCD=
| 1 |
| 2 |
| 2 |
∴VA-PCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| ||
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
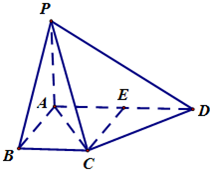 (一、二级达标校做)
(一、二级达标校做) .
.
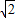 .
.