题目内容
(一、二级达标校做)
已知函数f(x)=2x+
(x∈R,λ∈R).
(Ⅰ) 讨论函数的f(x)奇偶性,并说明理由;
(Ⅱ)当λ=1时,讨论方程f(x)=μ(μ∈R)在x∈[-1,1]上实数解的个数情况,并说明理由.
已知函数f(x)=2x+
| λ |
| 2x |
(Ⅰ) 讨论函数的f(x)奇偶性,并说明理由;
(Ⅱ)当λ=1时,讨论方程f(x)=μ(μ∈R)在x∈[-1,1]上实数解的个数情况,并说明理由.
(Ⅰ)∵x∈R,定义域关于原点对称.
当λ=1时,f(-x)=2-x+
=2x+
=f(x),此时f(x)为偶函数.
当λ=-1时,f(-x)=2-x+
=
-2x=-f(x),此时f(x)为奇函数.
当λ≠±1时,f(-x)=2-x+
,显然f(-x)≠f(x),且 f(-x)≠-f(x),故f(x)为非奇非偶函数.
(Ⅱ)当λ=1时,f(x)=2x+
,方程f(x)=μ(μ∈R),即 2x+
=μ.
令t=2x,由于-1≤x≤1,∴
≤t≤2.
再由 g(t)=t+
在[
,1]上是减函数,在[1,2]上是增函数.
∴g(t)的最小值为g(1)=2,最大值为f(
)=
,或 g(2)=
,
故 g(t)的值域为[2,2],方程即t+
=μ.
当μ<2或μ>
时,解的个数为0;
当μ=2时,解的个数为1;
当2<μ≤
解的个数为2.
当λ=1时,f(-x)=2-x+
| 1 |
| 2-x |
| 1 |
| 2x |
当λ=-1时,f(-x)=2-x+
| -1 |
| 2-x |
| 1 |
| 2x |
当λ≠±1时,f(-x)=2-x+
| λ |
| 2-x |
(Ⅱ)当λ=1时,f(x)=2x+
| 1 |
| 2x |
| 1 |
| 2x |
令t=2x,由于-1≤x≤1,∴
| 1 |
| 2 |
再由 g(t)=t+
| 1 |
| t |
| 1 |
| 2 |
∴g(t)的最小值为g(1)=2,最大值为f(
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
故 g(t)的值域为[2,2],方程即t+
| 1 |
| t |
当μ<2或μ>
| 5 |
| 2 |
当μ=2时,解的个数为1;
当2<μ≤
| 5 |
| 2 |

练习册系列答案
相关题目
 (一、二级达标校做)
(一、二级达标校做) .
.
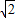 .
.