题目内容
12.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦点分别为F1,F2,且经过点$P({0,\sqrt{5}})$,离心率为$\frac{2}{3}$,A为直线x=4上的动点.(Ⅰ)求椭圆C的方程;
(Ⅱ)点B在椭圆C上,满足OA⊥OB,求线段AB长度的最小值.
分析 (Ⅰ)列出$\left\{\begin{array}{l}b=\sqrt{5}\\ e=\frac{c}{a}=\frac{2}{3}\\{a^2}={b^2}+{c^2}.\end{array}\right.$,然后求解椭圆方程.
(Ⅱ)点B在椭圆C上,设B(m,n),$n∈[{-\sqrt{5},0})∪({0,\sqrt{5}}]$,A(4,y).通过$\overrightarrow{OA}•\overrightarrow{OB}=0$,得到4m+ny=0.求出|AB|2的表达式,通过设t=n2,t∈(0,5],利用函数的导数求解函数的最小值.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}b=\sqrt{5}\\ e=\frac{c}{a}=\frac{2}{3}\\{a^2}={b^2}+{c^2}.\end{array}\right.$解得$\left\{\begin{array}{l}a=3\\ c=2.\end{array}\right.$,可得a=3,b=$\sqrt{5}$.
所以椭圆C的方程为$\frac{x^2}{9}+\frac{y^2}{5}=1$.
(Ⅱ)点B在椭圆C上,设B(m,n),$n∈[{-\sqrt{5},0})∪({0,\sqrt{5}}]$,A(4,y).
因为OA⊥OB,所以$\overrightarrow{OA}•\overrightarrow{OB}=0$,即4m+ny=0.
因为点B在椭圆C上,所以$\frac{m^2}{9}+\frac{n^2}{5}=1$,
所以|AB|2=(m-4)2+(n-y)2=m2-8m+16+n2-2ny+y2=m2-8m+16+n2+8m+y2,
=m2+16+n2+y2
=${m^2}+16+{n^2}+{({\frac{-4m}{n}})^2}$
=$9({1-\frac{n^2}{5}})+16+{n^2}+\frac{{16×9({1-\frac{n^2}{5}})}}{n^2}$,
=$\frac{144}{n^2}-\frac{{4{n^2}}}{5}-\frac{19}{5}$
设t=n2,t∈(0,5]
设$g(t)=\frac{144}{t}-\frac{4t}{5}-\frac{19}{5}$.
因为${g^'}(t)=\frac{-144}{t^2}-\frac{4}{5}<0$,
所以g(t)在(0,5]上单调递减.
所以当t=5,即$n=±\sqrt{5}$时,${|{AB}|_{min}}=\sqrt{21}$.
点评 本题考查椭圆的简单性质的应用,椭圆方程的求法,直线与椭圆的位置关系的综合应用,函数的导数求解函数的最值,考查转化思想以及计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | {4} | B. | {1,2,4,6,7} | C. | {3,5} | D. | {1,7} |
| A. | $\frac{4034}{4035}$ | B. | $\frac{2017}{4035}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
| A. | 6 | B. | 6$\sqrt{3}$ | C. | 12 | D. | 12$\sqrt{3}$ |
| A. | x2-4y2=1 | B. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{64}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-4x2=1 |
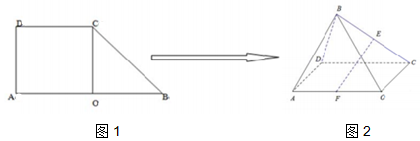
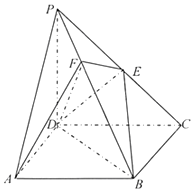 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.