题目内容
（10分） 已知抛物线
与直线
相交于A，B两点。
（1）求证：OA⊥OB；
（2）当
的面积等于
时，求
的值。
（1）见解析（2）
【解析】
试题分析：（1）将
转化为厁率之积等于
，即
，联立
，利用韦达定理得到
，再由
得证。（2） 
而
，利用韦达定理表示出来，解关于含
的方程。
试题解析：（1）证明：如图3，由方程组，消去x后，整理得
设
，由韦达定理知：
因为A、B在抛物线
上，所以
因为
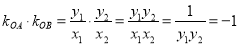，所以
（2）【解析】
连结AB，设直线AB与x轴交于N，由题意显然
令
，则
，即
因为
所以
因为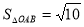
，所以
，解得
考点：直线与抛物线的综合问题
练习册系列答案
相关题目
，则“
”是“
的图象，只需将函数
的图象上所有点（ ）
个单位长度，再把横坐标缩短为原来的
倍（纵坐标不变）
个单位长度，再把横坐标缩短为原来的
B．
C．
D．
的渐近线方程为 （ ）
B．
C．
D．
=4,动点P满足
,则
的最小值为 .
的两个焦点F1，F2，点M在椭圆上，且
，
，
，则离心率
等于（ ）
B．
C．
D．
},则a+b=________．
的右焦点为
，过
的直线
交双曲线的渐近线于
、
两点，且直线
倾斜角的2倍，若
，则该双曲线的离心率为（ ）
B．
D．