题目内容
17.若acosθ-sinθ=1,asinθ+cosθ=1,则sinθ=-$\frac{1}{2}$或0.分析 将acosθ-sinθ=1,asinθ+cosθ=1分别平方相加得到a的值,重新代入等式求出sinθ的值即可.
解答 解:∵acosθ-sinθ=1,asinθ+cosθ=1,
∴a2cos2θ-2asinθcosθ+sin2θ=1①,
a2sin2θ+2asinθcosθ+cos2θ=1,②;
①+②解得:a=±1,
将a=±1代入①②,
解得:sinθ=-$\frac{1}{2}$或sinθ=0,
故答案为:-$\frac{1}{2}$或0.
点评 本题考查了事件恒等式的应用,考查三角函数求值问题,是一道基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8.sin$\frac{7}{6}$π=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
6.随机变量ξ的概率分布列为P(ξ=n)=a($\frac{4}{5}$)n(n=0.1.2),其中a为常数,则P(0.1<ξ<2.9)的值为( )
| A. | $\frac{16}{25}$. | B. | $\frac{9}{16}$ | C. | $\frac{36}{61}$ | D. | $\frac{20}{61}$ |
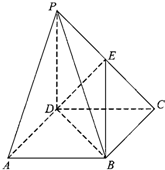 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.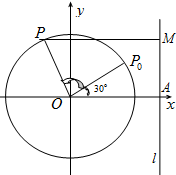 如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.
如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.