题目内容
已知函数 是定义在
是定义在 上的奇函数.
上的奇函数.
(Ⅰ)求 的值;
的值;
(Ⅱ)函数 的值域;
的值域;
(Ⅲ)当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
解:(Ⅰ)∵ 是奇函数
是奇函数
∴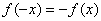
又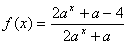
∴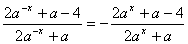 ,
,
即 对任意
对任意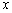 恒成立,
恒成立,
∴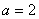
(或者利用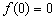 ,求得
,求得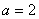 ,再验证是奇函数) …………………4分
,再验证是奇函数) …………………4分
(Ⅱ)∵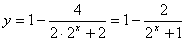
又∵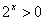 , ∴
, ∴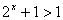
∴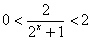 ,
,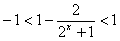
∴函数 的值域
的值域 ………………6分
………………6分
(Ⅲ)由题意得,当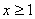 时,
时,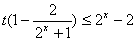
即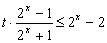 恒成立,
恒成立,
∵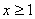 ,∴
,∴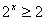 ,
,
∴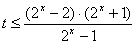 (
(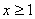 )恒成立, …………………8分
)恒成立, …………………8分
设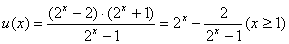
下证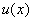 在当
在当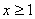 时是增函数.[来源:]
时是增函数.[来源:]
任取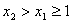 ,则
,则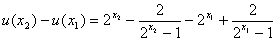
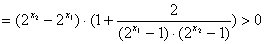 ………………………10分
………………………10分
∴当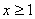 时,
时,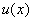 是增函数,
是增函数,
∴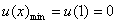
∴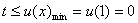
∴实数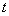 的取值范围为
的取值范围为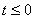 . …
. …

练习册系列答案
相关题目
某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:
| 非统计专业 | 统计专业 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
根据表中的数据断定主修统计专业与性别有关系,这种判断出错的可能性为____________.

 ,
, ,向量
,向量 ,
, 为实数,若
为实数,若 ,求
,求 ,山脚A处的俯角为
,山脚A处的俯角为 ,已知
,已知 ,则山的高度BC为 ( )
,则山的高度BC为 ( )
 , 设函数
, 设函数 .
. 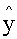 = x+1 B.
= x+1 B.  的前
的前 项和为
项和为 .若
.若 是
是 的等比中项,
的等比中项,  ,则
,则 等于 ( )
等于 ( )  B.
B. C.
C. D.
D.