题目内容
已知函数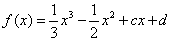 有极值.
有极值.
(1)求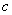 的取值范围;
的取值范围;
(2)若 在
在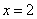
 处取得极值,且当
处取得极值,且当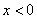 时,
时,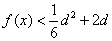 恒成立
恒成立 ,求
,求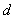 的取值范围.
的取值范围.
解:(1)∵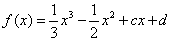 ,∴
,∴ 要使
要使 有极值,则方程
有极值,则方程 有两个实数解, 从而△=
有两个实数解, 从而△= ,∴
,∴
 .
.
(2)∵ 在
在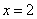 处取得极值, ∴
处取得极值, ∴ ,∴
,∴ .
.
∴ ,∵
,∵ ,
,
∴当 时,
时, ,函数单调递增,当
,函数单调递增,当
 时,
时, ,函数单调递减.
,函数单调递减.
∴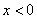 时,
时, 在
在 处取得最大值
处取得最大值 ,
,
∵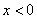 时,
时,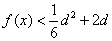 恒成立,∴
恒成立,∴
 ,即
,即 ,
,
∴ 或
或 ,即
,即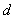
 的取值范围是
的取值范围是 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是R上的单调递减函数,则实数a的取值范围为( )
是R上的单调递减函数,则实数a的取值范围为( ) A.(-∞,2)
A.(-∞,2)  B.(-∞,
B.(-∞, ] C.(0,2)
] C.(0,2)  D.[
D.[ +4y2=4长轴上一个顶点为A,以A为直角顶点作一个内接于椭圆的等腰直角三角形,该三角形的面积是
+4y2=4长轴上一个顶点为A,以A为直角顶点作一个内接于椭圆的等腰直角三角形,该三角形的面积是  ,则
,则 为___
为___ 。
。 中
中 ,
, 是
是 中点.若
中点.若 ,则
,则 等于( )
等于( ) B、
B、 C、
C、 D、
D、
 ,其最小正周期为
,其最小正周期为 ,则
,则 ________.
________. ,则
,则 为___
为___