题目内容
O是坐标原点,P是椭圆
(ϕ为参数)上离心角为-
所对应的点,那么直线OP的倾斜角的正切值是 .
|
| π |
| 6 |
考点:椭圆的参数方程
专题:坐标系和参数方程
分析:由参数方程和离心角为-
求出点P的坐标,设直线OP的倾斜角为θ,由正切函数的定义得tanθ的值.
| π |
| 6 |
解答:
解:由题意得,P是椭圆
(ϕ为参数)上离心角为-
所对应的点,
所以点P的坐标为(3cos(-
),2sin(-
)),即P(
,-1),
设直线OP的倾斜角为θ,则tanθ=
=-
,
故答案为:-
.
|
| π |
| 6 |
所以点P的坐标为(3cos(-
| π |
| 6 |
| π |
| 6 |
3
| ||
| 2 |
设直线OP的倾斜角为θ,则tanθ=
| -1 | ||||
|
2
| ||
| 9 |
故答案为:-
2
| ||
| 9 |
点评:本题主要考查椭圆的参数方程,离心角的定义,正切函数的定义,以及直线的倾斜角,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
设抛物线的顶点在原点,准线方程为y=2,则抛物线的方程是( )
| A、x2=8y |
| B、x2=-8y |
| C、y2=-8x |
| D、y2=-8x |
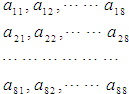 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=