题目内容
椭圆中心在原点，焦点在x轴上，离心率为
，点P（x，y）是椭圆上的一个动点，若
的最大值为10，求椭圆的标准方程．
解：设椭圆方程为
（a＞b＞0）
∵离心率e=
=，
∴a=2c，可得b2=a2-c2=3c2，得b=
c
点P（x，y）是椭圆上的一个动点，
设x=acosθ=2ccosθ，y=bsinθ=csinθ
∴=4ccosθ+3csinθ=5csin（θ+φ），其中tanφ=
∵的最大值为10，
∴5c=10，可得c=2，所以a=4，b=2
因此椭圆的标准方程为：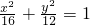
分析：设椭圆的方程为，由离心率算出a=2c且b=c，因此通过三角换元得=5csin（θ+φ），其中tanφ=．根据最大值为10得到c=2，由此即可得到该椭圆的标准方程．
点评：本题给出离心率为，其上一点P（x，y）满足的最大值为10的情况下求椭圆方程，着重考查了椭圆的基本概念、标准方程和简单几何性质等知识，属于基础题．
（a＞b＞0）∵离心率e=
=，∴a=2c，可得b2=a2-c2=3c2，得b=
c点P（x，y）是椭圆上的一个动点，
设x=acosθ=2ccosθ，y=bsinθ=
csinθ∴
=4ccosθ+3csinθ=5csin（θ+φ），其中tanφ=∵
的最大值为10，∴5c=10，可得c=2，所以a=4，b=2
因此椭圆的标准方程为：
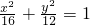
分析：设椭圆的方程为
，由离心率算出a=2c且b=c，因此通过三角换元得=5csin（θ+φ），其中tanφ=．根据最大值为10得到c=2，由此即可得到该椭圆的标准方程．点评：本题给出离心率为
，其上一点P（x，y）满足的最大值为10的情况下求椭圆方程，着重考查了椭圆的基本概念、标准方程和简单几何性质等知识，属于基础题． 
练习册系列答案
相关题目