题目内容
四棱锥P—ABCD的底面是边长为a的菱形,∠DAB=60°,PC⊥平面ABCD, PC=a,E是PA的中点,求点E到平面PBC的距离.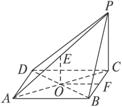
解析:设O是AC与BD的交点,则由E是PA的中点知EO∥PC,PC![]() 平面PBC,
平面PBC,
∴EO∥平面PBC.于是点O到平面PBC的距离等于E到平面PBC的距离.作OF⊥BC于F,
∵PC⊥平面ABCD,
∴平面PBC⊥平面ABCD.于是OF⊥平面PBC,OF的长等于O到平面PBC的距离.
∵底面是菱形,∠DAB=60°,
∴OB=![]() ,OF=
,OF=![]() a,即点E到平面PBC的距离为
a,即点E到平面PBC的距离为![]() a.
a.

练习册系列答案
相关题目
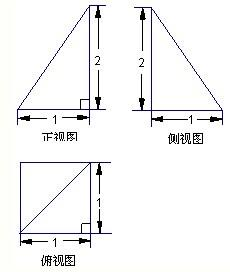 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
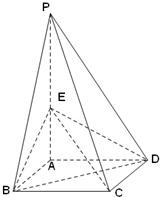 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: