题目内容

函数f(x)=Acos(ωx+
π
6
)+3（A＞0，ω＞0，x∈R）的最大值是5，周期为π．
（1）求A和ω的值；
（2）若θ∈（0，
π
3
)，f(θ)=
21
5
，求f(θ-
π
12
)的值．
分析：（1）由题意可得 A+3=5，由此求得A=2．再根据周期T=
2π
ω
=π，求得ω的值．
（2）由（1）可得 f(x)=2cos(2x+
π
6
)+3，根据f(θ)=
21
5
，求得cos(2θ+
π
6
) 的值，结合θ的范围，求得sin(2θ+
π
6
)的值，再利用两角和差的余项公式求得cos2θ的值，从而求得f(θ-
π
12
)=2cos2θ+3的值．
解答：解：（1）由题意可得 A+3=5，∴A=2．∵周期T=
2π
ω
=π，∴ω=2．
（2）由（1）可得 f(x)=2cos(2x+
π
6
)+3，∵f(θ)=2cos(2θ+
π
6
)+3=
21
5
，∴cos(2θ+
π
6
)=
3
5
．
又∵θ∈(0，
π
3
)，∴2θ+
π
6
∈(
π
6
，
5π
6
)，∴sin(2θ+
π
6
)=
1-cos2(2θ+
π
6
)
=
1-(
3
5
)2
=
4
5
．
∴cos2θ=cos[(2θ+
π
6
)-
π
6
]=cos(2θ+
π
6
)cos
π
6
+sin(2θ+
π
6
)sin
π
6
=
3
5
×
3
2
+
4
5
×
1
2
=
3
3
+4
10
，
∴f(θ-
π
12
)=2cos2θ+3=2×
3
3
+4
10
+3=
3
3
+19
5
．
点评：本题主要考查函数y=Asin（ωx+φ）的图象和性质，两角和差的余弦公式、同角三角函数的基本关系，属于中档题．
练习册系列答案
相关题目
已知定义在R上的函数f(x)=Acos(ωx+φ)(A＞0，ω＞0，|φ|≤
π
2
)，最大值与最小值的差为4，相邻两个最低点之间距离为π，且函数y=sin(2x+
π
3
)图象所有的对称中心都在y=f（x）图象的对称轴上．
（1）求f（x）的表达式；
（2）若f(
x0
2
)=
3
2
(x0∈[-
π
2
，
π
2
])，求cos(x0-
π
3
)的值；
（3）设
a
=(f(x-
π
6
)，1)，
b
=(1，mcosx)，x∈(0，
π
2
)，若
a
•
b
+3≥0恒成立，求实数m的取值范围．
已知函数f(x)=Acos (2ωx+2?)+2(A＞0，ω＞0，0＜?＜
π2
)的最大值为3，f（x）的图象的相邻两对称轴间的距离为2，在y轴上的截距为2．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设数列an=f（n），Sn为其前n项和，求S100．
（2012•广东）已知函数f(x)=Acos(
x
4
+
π
6
)，x∈R，且f(
π
3
)=
2

（1）求A的值；
（2）设α，β∈[0，
π
2
]，f(4α+
4
3
π)=-
30
17
，f(4β-
2
3
π)=
8
5
，求cos（α+β）的值．
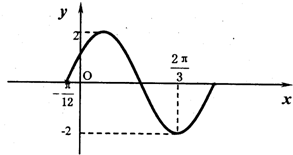精英家教网如图，给出函数f(x)=Acos(ωx+φ)(A＞0，|φ|＜
π2
)图象的一部分，则f（x）的解析式为f（x）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网