题目内容
(2012•包头一模)设函数f(x)=ln(x+1)+ae-x-a,a∈R.
(Ⅰ)当a=1时,证明f(x)在(0,+∞)是增函数;
(Ⅱ)若x∈[0,+∞),f(x)≥0,求a的取值范围.
(Ⅰ)当a=1时,证明f(x)在(0,+∞)是增函数;
(Ⅱ)若x∈[0,+∞),f(x)≥0,求a的取值范围.
分析:(1)求导函数,当a=1时,可得f′(x)=
,构造西红柿g(x)=ex-1-x,确定g(x)在(0,+∞)为增函数,从而可得x∈(0,+∞)时,g(x)>g(0)=0,由此可得x∈(0,+∞)时,f′(x)>0,得证;
(2)由于函数的最值不好确定,故进行适当的放缩,考虑f′(x)≥
=
,从而当1-a≥0,即a≤1时,对?x∈[0,+∞),f(x)≥f(0)=0;当a>1时,可得x∈(0,ln(a+
))时,f(x)<f(0)=0,从而可得a的取值范围.
| ex-(1+x) |
| ex(1+x) |
(2)由于函数的最值不好确定,故进行适当的放缩,考虑f′(x)≥
| 1+x-a(1+x) |
| ex(1+x) |
| (1-a)(1+x) |
| ex(1+x) |
| a2-a |
解答:解:(1)f′(x)=
-
=
,
当a=1时,f′(x)=
,---------(2分)
令g(x)=ex-1-x,则g′(x)=ex-1,
当x∈(0,+∞)时,g′(x)=ex-1>0,所以g(x)在(0,+∞)为增函数,
因此x∈(0,+∞)时,g(x)>g(0)=0,所以当x∈(0,+∞)时,f′(x)>0,
则f(x)在(0,+∞)是增函数.---------(6分)
(2)由f′(x)=
,
由(1)知,ex≥1+x,当且仅当x=0等号成立.
故f′(x)≥
=
,
从而当1-a≥0,即a≤1时,对x∈[0,+∞),f′(x)≥0,
于是对?x∈[0,+∞),f(x)≥f(0)=0.
由ex>1+x(x≠0),得e-x>1-x(x≠0),
从而当a>1时,
=
故当x∈(0,ln(a+
))时,f′(x)<0,
于是当x∈(0,ln(a+
))时,f(x)<f(0)=0,
综上,a的取值范围是(-∞,1].---------(12分)
| 1 |
| 1+x |
| a |
| ex |
| ex-a(1+x) |
| ex(1+x) |
当a=1时,f′(x)=
| ex-(1+x) |
| ex(1+x) |
令g(x)=ex-1-x,则g′(x)=ex-1,
当x∈(0,+∞)时,g′(x)=ex-1>0,所以g(x)在(0,+∞)为增函数,
因此x∈(0,+∞)时,g(x)>g(0)=0,所以当x∈(0,+∞)时,f′(x)>0,
则f(x)在(0,+∞)是增函数.---------(6分)
(2)由f′(x)=
| ex-a(1+x) |
| ex(1+x) |
由(1)知,ex≥1+x,当且仅当x=0等号成立.
故f′(x)≥
| 1+x-a(1+x) |
| ex(1+x) |
| (1-a)(1+x) |
| ex(1+x) |
从而当1-a≥0,即a≤1时,对x∈[0,+∞),f′(x)≥0,
于是对?x∈[0,+∞),f(x)≥f(0)=0.
由ex>1+x(x≠0),得e-x>1-x(x≠0),
从而当a>1时,
|
|
故当x∈(0,ln(a+
| a2-a |
于是当x∈(0,ln(a+
| a2-a |
综上,a的取值范围是(-∞,1].---------(12分)
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查学生分析解决问题的能力,正确求导是关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
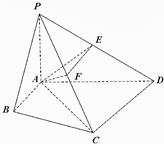 (2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
(2012•包头一模)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1. (2012•包头一模)函数f(x)=sin(ωx+?)(其中
(2012•包头一模)函数f(x)=sin(ωx+?)(其中