题目内容
已知椭圆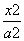 +
+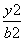 =1(a>b>0)经过点(0,
=1(a>b>0)经过点(0,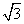 ),离心率为
),离心率为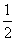 ,左右焦点分别为F1(-c,0),
,左右焦点分别为F1(-c,0),
F2(c,0).
(1)求椭圆的方程;
(2)若直线l:y=-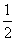 x+m与椭圆交于A,B两点,与以F1F2为直径的圆交于C,D两点,且满足
x+m与椭圆交于A,B两点,与以F1F2为直径的圆交于C,D两点,且满足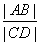 =
=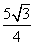 ,求直线l的方程.
,求直线l的方程.
解 (1)由题设知 解得a=2,b=
解得a=2,b=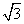 ,c=1.
,c=1.
∴椭圆的方程为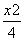 +
+ =1.
=1.
(2)由题设知,以F1F2为直径的圆的方程为x2+y2=1,
∴圆心到直线l的距离d= .
.
由d<1得|m|< .(*)
.(*)
 设A(x1,y1),B(x2,y2),
设A(x1,y1),B(x2,y2),
由 得x2-mx+m2-3=0.
得x2-mx+m2-3=0.
由根与系数的关系可得x1+x2=m,x1x2=m2-3.
 ∴直线l的方程为y=-
∴直线l的方程为y=-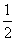 x+
x+ 或y=-
或y=-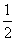 x-
x- .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 或k≤-4 B.-4≤k≤
或k≤-4 B.-4≤k≤ =1,长轴在y轴上.若焦距为4,则m等于( )
=1,长轴在y轴上.若焦距为4,则m等于( )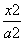 -
-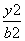 =1的右顶点作x轴的垂线,与C的一条渐近线相交于点A,若以C的右焦点为圆心,半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
=1的右顶点作x轴的垂线,与C的一条渐近线相交于点A,若以C的右焦点为圆心,半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( ) -
-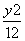 =1 B.
=1 B.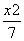 -
-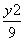 =1
=1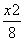 -
-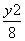 =1 D.
=1 D.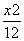 -
-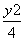 =1
=1 -
- 为( )
为( ) B.
B.
 D.
D.
 +y
+y 的最小值是________.
的最小值是________.