题目内容
已知
=(3,4),
=(4,3),求x,y的值使(x
+y
)⊥
,且|x
+y
|=1.
| a |
| b |
| a |
| b |
| a |
| a |
| b |
分析:由(x
+y
)⊥
,可得(x
+y
)•
=0,即 25x+24y=0 ①.再由|x
+y
|=1,可得 x(25x+24y)+24xy+25y2=1 ②.由①②可求得x,y的值.
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
解答:解:∵已知
=(3,4),
=(4,3),∴(x
+y
)=(3x+4y,4x+3y),
又(x
+y
)⊥
,∴(x
+y
)•
=3(3x+4y )+4(4x+3y)=0,即 25x+24y=0 ①.
再由|x
+y
|=1,可得 (3x+4y)2+(4x+3y)2=1,
整理得 25x2+48xy+25y2=1,即 x(25x+24y)+24xy+25y2=1 ②.
由①②有 24xy+25y2=1 ③,将①变形代入③可得:y=±
,
再代回①得:
和
.
| a |
| b |
| a |
| b |
又(x
| a |
| b |
| a |
| a |
| b |
| a |
再由|x
| a |
| b |
整理得 25x2+48xy+25y2=1,即 x(25x+24y)+24xy+25y2=1 ②.
由①②有 24xy+25y2=1 ③,将①变形代入③可得:y=±
| 5 |
| 7 |
再代回①得:
|
|
点评:本题主要考查两个向量的数量积公式的应用,两个向量垂直的性质,两个向量坐标形式的运算,向量的模的定义,属于中档题.

练习册系列答案
相关题目
已知a=(3,4),b⊥a,且b的起点为(1,2),终点为(x,3x),则b等于( )
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
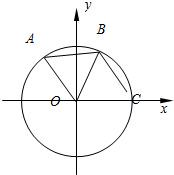 如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.
如图:A,B是圆O上的两点,点C是圆O与x轴正半轴的交点,已知A(-3,4),且点B在劣弧CA上,△AOB为正三角形.