题目内容
(本小题满分12分)已知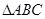 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,设向量
,设向量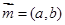 ,
, 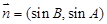 ,
, 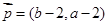
(Ⅰ)若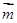 ∥
∥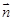 ,求证:
,求证: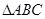 为等腰三角形;
为等腰三角形;
(Ⅱ)若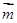 ⊥
⊥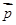 ,边长
,边长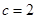 ,
,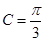 ,求
,求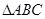 的面积.
的面积.
(Ⅰ)见解析;(Ⅱ) 。
。
解析试题分析:(Ⅰ) ∵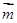 ∥
∥ , ∴
, ∴ ,由正弦定理可知,
,由正弦定理可知, ,其中R是
,其中R是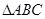 外接圆的半径,∴
外接圆的半径,∴ .因此,
.因此,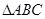 为等腰三角形.……6分
为等腰三角形.……6分
(Ⅱ)由题意可知, ,即
,即
由余弦定理可知, 即
即
 ,(
,( 舍去)∴
舍去)∴ .…………12分
.…………12分
考点:正弦定理;平面向量数量积的运算;三角形的面积公式。
点评:本题以向量的方式来给出题设条件,来考查三角有关的知识,较为综合。同时本题对答题者公式掌握的熟练程度要求较高,是一道中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
与向量
 平行的单位向量为( ).
平行的单位向量为( ).
A. |
B. |
C. 或 或 |
D. 或 或 |
在 中,有如下四个命题:①
中,有如下四个命题:① ; ②
; ②
 ;③若
;③若 ,则
,则 为等腰三角形;④若
为等腰三角形;④若 ,则
,则 为锐角三角形.其中正确的命题序号是( )
为锐角三角形.其中正确的命题序号是( )
| A.① ② | B.① ③ ④ | C.② ③ | D.② ④ |
 ,函数
,函数
 ·
· ,
, .
. 的值;
的值; 
 ,求
,求 的值.
的值.  ,求函数f(x)的值域;
,求函数f(x)的值域;
 时,求
时,求 的值;
的值;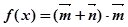 ,求
,求 的单调增区间;
的单调增区间; 中,
中, 分别为角
分别为角 的对边,
的对边, ,对于(2)中的函数
,对于(2)中的函数 的取值范围。
的取值范围。 ,设函数
,设函数 ,(Ⅰ)求函数
,(Ⅰ)求函数 的表达式;(Ⅱ)在
的表达式;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若
 ,
, ,
, ,求边
,求边 的长.
的长. ;(1)求:AB2+AC2的值;(2)当△ABC的面积最大时,求A的大小.
;(1)求:AB2+AC2的值;(2)当△ABC的面积最大时,求A的大小. ,点B
,点B ,若点C在直线
,若点C在直线 上,且
上,且 .
. 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为 。
。 ;
;
 ,求
,求 的取值范围。
的取值范围。