题目内容
7.已知向量$\overrightarrow a=({sin({2x+\frac{π}{6}}),1})$,$\overrightarrow b=({\sqrt{3},cos({2x+\frac{π}{6}})})$,函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.(Ⅰ)求函数f(x)的单调递减区间;
(Ⅱ)在△ABC中,A、B、C的对边分别是a、b、c,若$f(A)=\sqrt{3},sinC=\frac{1}{3},a=3$,求b的值.
分析 (Ⅰ)化简f(x)=2sin(2x+$\frac{π}{3}$),从而可得2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,从而解得;
(Ⅱ)化简可得A=$\frac{π}{6}$;再由sinC=$\frac{1}{3}$可得C<$\frac{π}{6}$,cosC=$\frac{2\sqrt{2}}{3}$,从而利用正弦定理求解.
解答 解:(Ⅰ)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}$sin(2x+$\frac{π}{6}$)+cos(2x+$\frac{π}{6}$)
=2sin(2x+$\frac{π}{3}$),
当2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,
即kπ+$\frac{π}{12}$≤x≤kπ+$\frac{7π}{12}$,(k∈Z),
函数f(x)单调递减,
故函数f(x)的单调递减区间为[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$],(k∈Z);
(Ⅱ)f(A)=2sin(2A+$\frac{π}{3}$)=$\sqrt{3}$,
∴sin(2A+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,
∴2A+$\frac{π}{3}$=2kπ+$\frac{π}{3}$或2A+$\frac{π}{3}$=2kπ+$\frac{2π}{3}$,
∴A=kπ或A=kπ+$\frac{π}{6}$,(k∈Z);
又∵A∈(0,π),∴A=$\frac{π}{6}$;
∵sinC=$\frac{1}{3}$,C∈(0,π),sinA=$\frac{1}{2}$,
∴C<$\frac{π}{6}$,cosC=$\frac{2\sqrt{2}}{3}$,
∴sinB=sin(A+C)=$\frac{\sqrt{3}+2\sqrt{2}}{6}$,
∴b=$\frac{3sinB}{sinA}$=$\sqrt{3}$+2$\sqrt{2}$.
点评 本题考查了平面向量的应用及三角恒等变换的应用,同时考查了解三角形的应用.

| A. | $\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 | B. | $\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1 | C. | $\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1 | D. | $\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1 |
| A. | $\frac{\sqrt{2}}{4}$倍 | B. | $\frac{1}{2}$倍 | C. | $\frac{\sqrt{2}}{2}$倍 | D. | $\sqrt{2}$倍 |
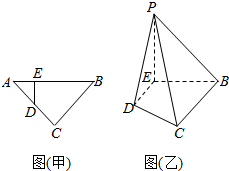 如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙))
如图(甲),等腰直角三角形的底边AB=4,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图(乙)) 已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.
已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.