题目内容
2.已知p:?x∈R,不等式x2-mx+$\frac{3}{2}$>0恒成立,q:椭圆$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{3-m}$=1的焦点在x轴上,若“p或q”为真,“p且q”为假,求实数m的取值范围.分析 分别判断出p,q为真时的m的范围,通过讨论p,q的真假,得到关于m的不等式组,取并集即可.
解答 解:∵p:?x∈R,不等式x2-mx+$\frac{3}{2}$>0恒成立,
∴△=m2-6<0,解得:-$\sqrt{6}$<m<$\sqrt{6}$;
q:椭圆$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{3-m}$=1的焦点在x轴上,
∴m-1>3-m>0,解得:2<m<3,
若“p或q”为真,“p且q”为假,
则:p,q一真一假,
p真q假时:$\left\{\begin{array}{l}{-\sqrt{6}<m<\sqrt{6}}\\{m≥3或m≤2}\end{array}\right.$,解得:-$\sqrt{6}$<m<2,
p假q真时:$\left\{\begin{array}{l}{m≥\sqrt{6}或m≤-\sqrt{6}}\\{2<m<3}\end{array}\right.$,解得:$\sqrt{6}$≤m<3,
故m的范围是(-$\sqrt{6}$,2)∪[$\sqrt{6}$,3).
点评 本题考查了复合命题的真假,考查不等式恒成立问题,考查椭圆问题,是一道基础题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
11.当-$\frac{π}{2}$≤x≤$\frac{π}{2}$时,函数f(x)=2sin(x+$\frac{π}{3}$)有( )
| A. | 最大值1,最小值-1 | B. | 最大值1,最小值-$\frac{1}{2}$ | ||
| C. | 最大值2,最小值-2 | D. | 最大值2,最小值-1 |
7.已知命题p:?x∈(0,$\frac{π}{2}$),使得cosx≥x,则该命题的否定是( )
| A. | ?x∈(0,$\frac{π}{2}$),使得cosx>x | B. | ?x∈(0,$\frac{π}{2}$),使得cosx≥x | ||
| C. | ?x∈(0,$\frac{π}{2}$),使得cosx<x | D. | ?x∈(0,$\frac{π}{2}$),使得cosx<x |
11.球O半径为R=13,球面上有三点A、B、C,AB=12$\sqrt{3}$,AC=BC=12,则四面体OABC的体积是( )
| A. | 60$\sqrt{3}$ | B. | 50$\sqrt{3}$ | C. | 60$\sqrt{6}$ | D. | 50$\sqrt{6}$ |
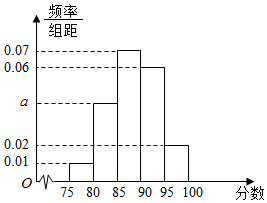 某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].
某地区有100名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:第1组:[75,80),第2组:[80,85),第3组:[85,90),第4组:[90,95),第5组:[95,100].