题目内容
求矩阵M=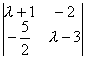 的特征值和特征向量.
的特征值和特征向量.
思路点拨:要计算矩阵的特征值和特征向量,关键是计算矩阵对应的行列式的值,然后再代入相应的公式即可.
解:矩阵M的特征值λ满足方程:
0=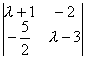 =(λ+1)(λ-3)-(-
=(λ+1)(λ-3)-(-![]() )(-2),即λ2-2λ-8=0.
)(-2),即λ2-2λ-8=0.
解得矩阵M的两个特征值λ1=4,λ2=-2.
(1)设属于特征值λ1=4的特征向量为![]() ,则它满足方程(λ1+1)x+(-2)y=0,即(4+1)x+(-2)y=0,也就是5x-2y=0,则可取
,则它满足方程(λ1+1)x+(-2)y=0,即(4+1)x+(-2)y=0,也就是5x-2y=0,则可取![]() 为属于特征值λ1=4的一个特征向量.
为属于特征值λ1=4的一个特征向量.
(2)设属于特征值λ2=-2的特征向量为![]() ,则它满足方程(λ2+1)x+(-2)y=0,即(-2+1)x+(-2)y=0,也就是x+2y=0,则可取
,则它满足方程(λ2+1)x+(-2)y=0,即(-2+1)x+(-2)y=0,也就是x+2y=0,则可取![]() 为属于特征值λ2=-2的一个特征向量.
为属于特征值λ2=-2的一个特征向量.
综上所述:M=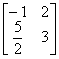 有两个特征值λ1=4,λ2=-2,属于λ1=4的一个特征向量为
有两个特征值λ1=4,λ2=-2,属于λ1=4的一个特征向量为![]() ,属于λ2=-2的一个特征向量为
,属于λ2=-2的一个特征向量为![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
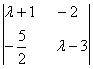 的特征值和特征向量.
的特征值和特征向量. ,(Ⅰ)求M-1;(Ⅱ)求矩阵M的特征值和对应的特征向量;(Ⅲ)计算M100β.
,(Ⅰ)求M-1;(Ⅱ)求矩阵M的特征值和对应的特征向量;(Ⅲ)计算M100β. .
.