题目内容

选做题 (矩阵与变换)

求矩阵M=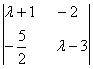的特征值和特征向量.

解:矩阵M的特征值λ满足方程

0=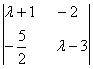=(λ+1)(λ-3)-()(-2)=λ2-2λ-8,

解得,矩阵M的两个特征值λ1=4,λ2=-2,

(1)设属于特征值λ1=4的特征向量为,则它满足方程(λ1+1)x+(-2)y=0,即(4+1)x+(-2)y=0,也就是5x-2y=0,

则可取为属于特征值λ1=4的一个特征向量.

(2)设属于特征值λ1=-2的特征向量为,则它满足方程(λ2+1)x+(-2)y=0,

即(-2+1)x+(-2)y=0,也就是x+2y=0,

则可取为属于特征值λ2=-2的一个特征向量.

综上所述:M=有两个特征值λ1=4,λ2=-2,

属于λ1=4的一个特征向量为,属于λ2=-2的一个特征向量为.

练习册系列答案
相关题目
本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．
（1）选修4-2：矩阵与变换
已知矩阵A=
33
cd
，若矩阵A属于特征值6的一个特征向量为
α
=
1
1
，属于特征值1的一个特征向量为
β
=
^ 
&-2；
（Ⅰ）求矩阵A；
（Ⅱ）判断矩阵A是否可逆，若可逆求出其逆矩阵A-1．
（2）选修4-4：坐标系与参数方程
已知直线的极坐标方程为ρsin(θ+
π
4
)=
2
2
，圆M的参数方程为
x=2cosθ
y=-2+2sinθ
（其中θ为参数）．
（Ⅰ）将直线的极坐标方程化为直角坐标方程；
（Ⅱ）求圆M上的点到直线的距离的最小值．
（3）选修4-5：不等式选讲，设函数f（x）=|x-1|+|x-a|；
（Ⅰ）若a=-1，解不等式f（x）≥3；
（Ⅱ）如果关于x的不等式f（x）≤2有解，求a的取值范围．
选做题：在A、B、C、D四小题中只能选做2题，每小题10分，共20分．解答应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，PA切⊙O于点A，D为PA的中点，过点D引割线交⊙O于B、C两点．求证：∠DPB=∠DCP．
B．选修4-2：矩阵与变换
设M=
.
10
02
.
，N=
.
1
2
0
01
.
，试求曲线y=sinx在矩阵MN变换下的曲线方程．
C．选修4-4：坐标系与参数方程
在极坐标系中，圆C的极坐标方程为ρ=
2
cos(θ+
π
4
)，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
4
5
t
y=-1-
3
5
t
（t为参数），求直线l被圆C所截得的弦长．
D．选修4-5：不等式选讲
解不等式：|2x+1|-|x-4|＜2．
选作题，本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．（几何证明选讲）
如图，AB是半圆的直径，C是AB延长线上一点，CD切半圆于点D，CD=2，DE⊥AB，垂足为E，且E是OB的中点，求BC的长．
B．（矩阵与变换）
已知矩阵
12
2a
的属于特征值b的一个特征向量为
1
1
，求实数a、b的值．
C．（极坐标与参数方程）
在平面直角坐标系xOy中，已知点A（1，-2）在曲线
x=2pt2
y=2pt
（t为参数，p为正常数），求p的值．
D．（不等式选讲）
设a1，a2，a3均为正数，且a1+a2+a3=1，求证：
1
a1
+
1
a2
+
1
a3
≥9．
选做题 
（1）已知a，b∈R，若M=
-1a
b3
所对应的变换TM把直线L：2x-y=3变换为自身，求实数a，b，并求M的逆矩阵．
（2）已知直线l的参数方程为
x=
1
2
t
y=
2
2
+
3
2
t
（t为参数），若以直角坐标系xOy的O点为极点，Ox方向为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程为ρ=2cos（θ-
π
4
）．
（Ⅰ）求直线l的倾斜角；
（Ⅱ）若直线l与曲线C交于A，B两点，求|AB|．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网