题目内容
数列{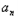 }首项a1=1,前n项和
}首项a1=1,前n项和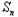 与
与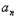 之间满足
之间满足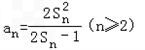 .
.
(1)求证:数列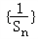 是等差数列;
是等差数列;
(2)求数列{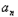 }的通项公式;
}的通项公式;
(3)设存在正数k,使 对一切n∈N*都成立,求k的最大值.
对一切n∈N*都成立,求k的最大值.
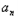 }首项a1=1,前n项和
}首项a1=1,前n项和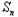 与
与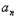 之间满足
之间满足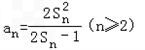 .
.(1)求证:数列
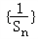 是等差数列;
是等差数列;(2)求数列{
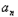 }的通项公式;
}的通项公式;(3)设存在正数k,使
 对一切n∈N*都成立,求k的最大值.
对一切n∈N*都成立,求k的最大值.(1)证明:∵n≥2时,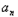 =
=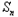 ﹣
﹣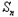 ﹣1
﹣1
∴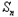 -
-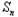 -1=
-1=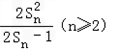
∴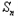 -1﹣
-1﹣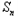 =2
=2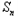 ·
·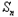 -1
-1
∴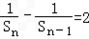 (n≥2)
(n≥2)
∴数列{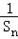 |是以
|是以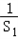 =1为首项,以2为公差的等差数列
=1为首项,以2为公差的等差数列
(2)解:由(1)知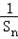 =1+(n﹣1)×2=2n﹣1,
=1+(n﹣1)×2=2n﹣1,
∴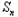 =
=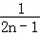 ,
,
∴n≥2时,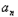 =
=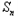 ﹣
﹣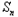 ﹣1=﹣
﹣1=﹣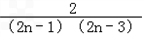
∵a1=S1=1,
∴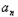 =
=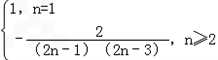 .
.
(3)设F(n)=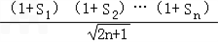 ,
,
则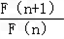 =
=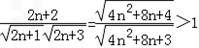
∴F(n)在n∈N*上递增,要使F(n)≥k恒成立,
只需[F(n)]min≥k
∵[F(n)]min=F(1)=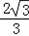 ,
,
∴0<k≤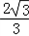 ,kmax=
,kmax=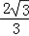
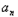 =
=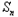 ﹣
﹣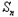 ﹣1
﹣1∴
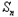 -
-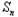 -1=
-1=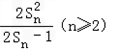
∴
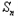 -1﹣
-1﹣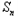 =2
=2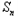 ·
·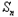 -1
-1∴
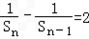 (n≥2)
(n≥2)∴数列{
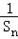 |是以
|是以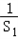 =1为首项,以2为公差的等差数列
=1为首项,以2为公差的等差数列(2)解:由(1)知
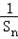 =1+(n﹣1)×2=2n﹣1,
=1+(n﹣1)×2=2n﹣1,∴
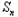 =
=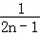 ,
,∴n≥2时,
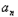 =
=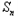 ﹣
﹣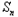 ﹣1=﹣
﹣1=﹣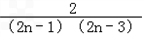
∵a1=S1=1,
∴
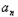 =
=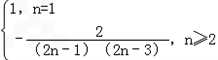 .
.(3)设F(n)=
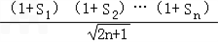 ,
,则
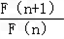 =
=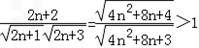
∴F(n)在n∈N*上递增,要使F(n)≥k恒成立,
只需[F(n)]min≥k
∵[F(n)]min=F(1)=
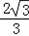 ,
,∴0<k≤
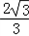 ,kmax=
,kmax=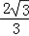

练习册系列答案
相关题目