Question

已知复数（x-2）+yi（x，y∈R）的模为

3

，则

y

x

的最大值是（　　）

• A、

  3

  2

• B、

  3

  3

• C、

  1

  2

• D、

  3

Answer 1

分析：根据复数（x-2）+yi（x，y∈R）的模为

3

得：（x-2）²+y²=3，根据

y

x

的几何意义：表示动点（x，y）到定点（0，0）的斜率．根据图形求解．

解答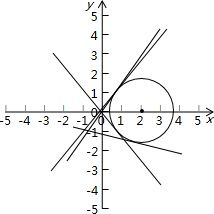：解：∵复数（x-2）+yi（x，y∈R）的模为

3

∴（x-2）²+y²=3
根据

y

x

的几何意义：表示动点（x，y）到定点（0，0）的斜率知：

y

x

的最大值是：

3

故选D

点评：本题考查复数的基本概念，复数求模，简单线性规划，解答关键是数形结合能力、计算能力，是中档题．