题目内容
(本小题满分11分)
已知函数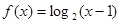 ,
,
(1)求函数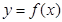 的定义域;
的定义域;
(2)设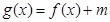 ,若函数
,若函数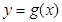 在(2,3)内有且仅有一个零点,求实数
在(2,3)内有且仅有一个零点,求实数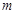 的取值范围;
的取值范围;
(3)设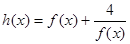 ,求函数
,求函数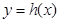 在[3,9]内的值域;
在[3,9]内的值域;
已知函数
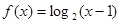 ,
,(1)求函数
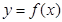 的定义域;
的定义域;(2)设
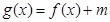 ,若函数
,若函数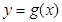 在(2,3)内有且仅有一个零点,求实数
在(2,3)内有且仅有一个零点,求实数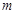 的取值范围;
的取值范围;(3)设
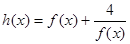 ,求函数
,求函数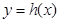 在[3,9]内的值域;
在[3,9]内的值域;(1){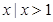 };(2)
};(2)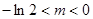 ;(3)
;(3)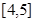 .
.
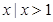 };(2)
};(2)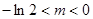 ;(3)
;(3)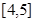 .
.(1)根据对数的真数大于零列不等式求解即可;(2)利用零点存在性定理列出关于参数m的不等式,然后利用不等式知识求解即可;(3)利用函数的单调性求出函数的最值(值域)
解:(1)由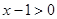 得,
得,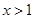 ,故所求函数的定义域为{
,故所求函数的定义域为{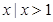 };
};
(2)因为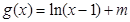 在(2,3)内有且仅有一个零点,所以
在(2,3)内有且仅有一个零点,所以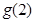 ·
·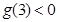 ,即
,即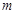 ·
·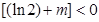 ,得
,得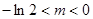 ;
;
(3)易求得,在[3,9]内,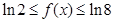 ,所以
,所以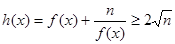
可见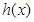 取最小值的条件是
取最小值的条件是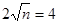 ,解得
,解得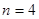 ,此时
,此时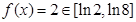 ,故存在实数
,故存在实数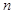 ,使得函数
,使得函数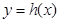 在[3,9]内的最小值为4;而
在[3,9]内的最小值为4;而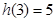 ,
,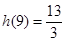 ,故函数
,故函数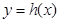 在[3,9]内的值域为
在[3,9]内的值域为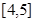 ;
;
解:(1)由
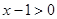 得,
得,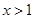 ,故所求函数的定义域为{
,故所求函数的定义域为{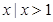 };
};(2)因为
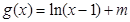 在(2,3)内有且仅有一个零点,所以
在(2,3)内有且仅有一个零点,所以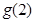 ·
·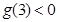 ,即
,即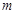 ·
·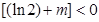 ,得
,得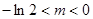 ;
;(3)易求得,在[3,9]内,
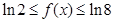 ,所以
,所以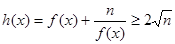
可见
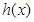 取最小值的条件是
取最小值的条件是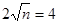 ,解得
,解得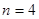 ,此时
,此时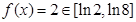 ,故存在实数
,故存在实数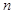 ,使得函数
,使得函数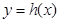 在[3,9]内的最小值为4;而
在[3,9]内的最小值为4;而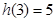 ,
,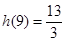 ,故函数
,故函数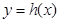 在[3,9]内的值域为
在[3,9]内的值域为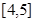 ;
;
练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
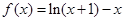
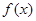 的单调递减区间;
的单调递减区间;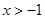 ,证明:
,证明: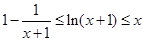 .
. 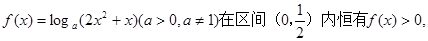 则f(x)的单调递增区间是
则f(x)的单调递增区间是 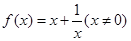 是( )
是( ) 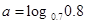 ,
,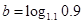 ,
,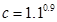 ,那么( )
,那么( )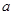 <b<c
<b<c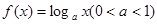 在区间
在区间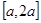 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则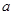


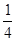

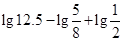 的值.
的值.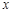 满足
满足 ,则
,则 的值为 .
的值为 .