题目内容
【题目】已知
，
（1）若展开式中第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大项
的系数；
（2）若展开式前三项的二项式系数和等于79，求展开式中系数最大的项．
【答案】（1）70（2）
（2x）10
【解析】
试题分析：（1）第k+1项的二项式系数为
，由题意可得关于n的方程，求出n．而二项式系数最大的项为中间项，n为奇数时，中间两项二项式系数相等；n为偶数时，中间只有一项．（2）由展开式前三项的二项式系数和等于79，可得关于n的方程，求出n．而求展开式中系数最大的项时，可通过解不等式组求得，假设
项的系数最大，
项的系数为
，则有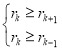
试题解析：（1）通项Tr＋1＝
n－r·（2x）r＝22r－n
xr，（此题可以用组合数表示结果）
由题意知
，
，
成等差数列，
∴
＝
，∴n＝14或7.
当n＝14时，第8项的二项式系数最大，该项的系数为22×7－14
＝3 432；
当n＝7时，第4、5项的二项式系数相等且最大，
其系数分别为22×3－7
=
，22×4－7
=70.
（2）由题意知
＝79，
∴n＝12或n＝－13（舍）．
∴Tr＋1＝22r－12
xr.
由
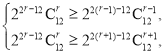得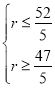
∴r＝10.
∴展开式中系数最大的项为T11＝22×10－12·
（2x）10.
练习册系列答案
阅读快车系列答案
相关题目
