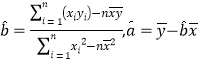题目内容
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为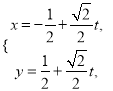 椭圆
椭圆![]() 的参数方程为
的参数方程为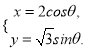 在以坐标原点为极点,
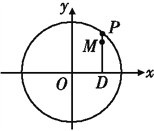
在以坐标原点为极点, ![]() 轴正半轴为极轴建立的极坐标系中,点
轴正半轴为极轴建立的极坐标系中,点![]() 的坐标为
的坐标为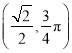 .
.
(1)将点![]() 的坐标化为直角坐标系下的坐标,椭圆的参数方程化为普通方程;
的坐标化为直角坐标系下的坐标,椭圆的参数方程化为普通方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() ;
; ![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)根据直角坐标与极坐标的互化公式,即可得到![]() 点直角坐标系下的坐标;
点直角坐标系下的坐标;
消去参数,即可得到椭圆的普通方程.
(2)将直线的参数方程代入椭圆的方程中,化简得![]() ,根据韦达定理得到
,根据韦达定理得到![]() 的值,即可利用参数的几何意义,求解
的值,即可利用参数的几何意义,求解![]() 的值.
的值.
试题解析:
(1)因为![]() 的极坐标为
的极坐标为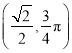 ,所以
,所以![]() ,
, ![]() ,
,
所以![]() 点直角坐标系下的坐标为
点直角坐标系下的坐标为![]() ;
;
由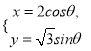 可得
可得![]() .
.
(2)点![]() 作直线
作直线![]() 上,将
上,将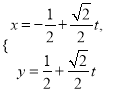 代入
代入![]() 化简得
化简得![]() ;
;
显然![]() ,设此方程两根为
,设此方程两根为![]() ,
, ![]() ,则
,则![]() ,
,
由参数![]() 的几何意义得
的几何意义得![]() .
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
【题目】某厂需要确定加工某大型零件所花费的时间,连续4天做了4次统计,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 5.5 |
(1)在直角坐标系中画出以上数据的散点图,求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(2)试预测加工10个零件需要多少时间?
参考公式:两个具有线性关系的变量的一组数据:![]() ,
,
其回归方程为![]() ,其中
,其中