题目内容
17.设函数$f(x)=\sqrt{ln(x+1)+2x-a}$(a∈R).若存在x0∈[0,1]使得f(f(x0))=x0,则a的取值范围是[-1,2+ln2].分析 由f(f(x0))=x0得f-1(x0)=f(x0),
根据f(x)与f-1(x)的对称关系可得f(x0)=x0,
于是f(x0)∈[0,1],分离参数得到a的范围.
解答 解:∵f(f(x0))=x0,
∴f-1(x0)=f(x0),
∵f-1(x)和f(x)关于直线y=x对称,
∴f(x0)=x0,
∵x0∈[0,1],
∴0≤$\sqrt{ln{(x}_{0}+1)+{2x}_{0}-a}$≤1,
即0≤ln(x0+1)+2x0-a≤1.
∴-[ln(x0+1)+2x0]≤-a≤1-[ln(x0+1)+2x0]
∴[ln(x0+1)+2x0]-1≤a≤ln(x0+1)+2x0]
∵存在x0∈[0,1]使f(f(x0))=x0,
∴-1≤a≤2+ln2.
故答案为:[-1,2+ln2].
点评 本题考查了反函数的性质以及函数最值的应用问题,是较难的题目.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
8.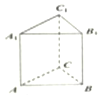 如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )
 如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1中,∠CAB=90°,AC=AB=AA1,则异面直线AC1,A1B所成角的余弦值为( )| A. | $-\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
12.在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(“倍加增”指灯的数量从塔的顶层到底层按公比为2的等比数列递增).根据此诗,可以得出塔的顶层和底层共有( )
| A. | 3盏灯 | B. | 192盏灯 | C. | 195盏灯 | D. | 200盏灯 |
6.△ABC的内角A,B,C的对边分别为a,b,c,已知cosC=$\frac{1}{4}$,a=1,c=2,则△ABC的面积为( )
| A. | $\frac{\sqrt{15}}{4}$ | B. | $\frac{\sqrt{15}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |