题目内容
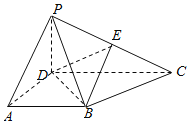
【题目】如图,在四棱锥![]() 中,
中,![]() 平面ABCD,底面ABCD为梯形,
平面ABCD,底面ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,E为PC的中点.
,E为PC的中点.
![]() 证明:
证明:![]() 平面PAD;
平面PAD;
![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
![]() 设F为PD的中点,连接EF,
设F为PD的中点,连接EF,![]() 证明
证明![]() ,推出四边形ABEF为平行四边形,所以
,推出四边形ABEF为平行四边形,所以![]() 然后证明
然后证明![]() 平面PAD.
平面PAD.
![]() 取AB中点M,连接DM,证明
取AB中点M,连接DM,证明![]() ,以DM、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,求出平面PBC的一个法向量,平面PCD的一个法向量,设二面角
,以DM、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,求出平面PBC的一个法向量,平面PCD的一个法向量,设二面角![]() 的平面角为
的平面角为![]() ,利用空间向量的数量积求解即可
,利用空间向量的数量积求解即可
![]() 证明:设F为PD的中点,连接EF,FA.
证明:设F为PD的中点,连接EF,FA.
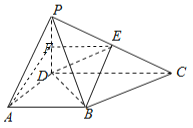
因为EF为![]() 的中位线,所以
的中位线,所以![]() ,
,
且![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,且
,且![]()
故四边形ABEF为平行四边形,所以![]() .
.
又![]() 平面PAD,
平面PAD,![]() 平面PAD,所以
平面PAD,所以![]() 平面
平面![]()
![]() 解:取AB中点M,连接DM
解:取AB中点M,连接DM
![]() ,
,![]() ,
,
![]() 为等边三角形
为等边三角形
从而,中线![]() ,且
,且![]() ,
,
又![]() ,故D
,故D![]()
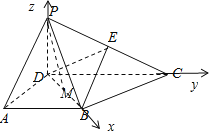
如图所示,
以DM、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
![]() ,
,![]()
![]() ,
,![]() 4,
4,![]() ,
,![]() 0,
0,![]()
于是![]() ,
,![]()
设平面PBC的一个法向量为![]() y,
y,![]()
则![]() ,
,![]() ,从而
,从而![]() ,
,![]()
![]() ,解得
,解得![]()
令![]() ,得
,得![]() ,且
,且![]()
易知,平面PCD的一个法向量为![]() ,且
,且![]()
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() .
.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】为考察某种疫苗预防疾病的效果,进行动物试验,得到统计数据如下:现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 | x | A |
注射疫苗 | 40 | y | B |
总计 | 60 | 40 | 100 |
(1)求2×2列联表中的数据x,y,A,B的值.
(2)能否在犯错误的概率不超过0.01的前提下认为疫苗有效?
附:![]()
临界值表:
P(K2≥k0) | 0.05 | 0.01 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.28 | 4.72 | 3.58 | 2.70 | 2.15 |
倒闭企业所占比例 | 21.4% | 19.1% | 14.5% | 10.9% | 8.7% |
(1)由所给数据可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年成立的企业中倒闭企业所占比例.
年成立的企业中倒闭企业所占比例.
参考数据:![]() ,
,![]() ,
,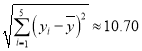 ,
,![]() ,
,
相关系数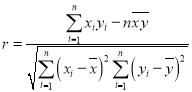 ,样本
,样本![]() 的最小二乘估计公式为
的最小二乘估计公式为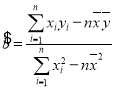 ,
,![]() .
.