题目内容
4.已知正项数列{an},前n项和为Sn,且有$\sqrt{{S}_{n}}$=λan+c.(1)求证:λc≤$\frac{1}{4}$;
(2)若λ=1,c=0,求证:Sn≥($\frac{n+1}{2}$)2;
(3)若2a2=a1+a3,求证:{an}为等差数列.
分析 (1)由$\sqrt{{S}_{n}}$=λan+c,可得n=1时,a1=$(λ{a}_{1}+c)^{2}$,化为${λ}^{2}{a}_{1}^{2}$+(2λc-1)a1+c2=0,λ=0时,此时λc≤$\frac{1}{4}$;当λ≠0时,△≥0,解出即可证明.
(2)λ=1,c=0,可得:$\sqrt{{S}_{n}}$=an,即Sn=${a}_{n}^{2}$.利用数学归纳法即可证明.
(3)令a2-a1=d>0,由已知可得:$\sqrt{{a}_{1}}$=λa1+c,$\sqrt{{a}_{1}+{a}_{2}}=λ{a}_{2}$+c,$\sqrt{{a}_{1}+{a}_{2}+{a}_{3}}$=λa3+c,化简整理即可把λ,c,a1都用d表示,再利用递推关系即可得出.
解答 证明:(1)∵$\sqrt{{S}_{n}}$=λan+c,∴n=1时,a1=$(λ{a}_{1}+c)^{2}$,
化为${λ}^{2}{a}_{1}^{2}$+(2λc-1)a1+c2=0,
λ=0时,化为${a}_{1}={c}^{2}$,此时λc≤$\frac{1}{4}$;
当λ≠0时,△=(2λc-1)2-4λ2c2≥0,解得λc≤$\frac{1}{4}$.
综上可得:λc≤$\frac{1}{4}$成立.
(2)λ=1,c=0,可得:$\sqrt{{S}_{n}}$=an,即Sn=${a}_{n}^{2}$.
利用数学归纳法证明:①当n=1时,${a}_{1}={a}_{1}^{2}$>0,解得a1=1,a1≥$(\frac{1+1}{2})^{2}$=1成立.
②假设当n=k(k∈N*)时,${S}_{k}={a}_{k}^{2}$≥$(\frac{k+1}{2})^{2}$,即${a}_{k}≥\frac{k+1}{2}$成立.
则n=k+1时,Sk+1=Sk+ak+1,
∴${a}_{k+1}^{2}$-ak+1=${S}_{k}={a}_{k}^{2}$≥$(\frac{k+1}{2})^{2}$,
∴${a}_{k+1}^{2}$-ak+1-$(\frac{k+1}{2})^{2}$≥0,解得ak+1≥$\frac{(k+1)+1}{2}$,
因此Sk+1≥$(\frac{k+1+1}{2})^{2}$成立.
综上可得:Sn≥($\frac{n+1}{2}$)2对于?n∈N*成立.
(3)令a2-a1=d>0,
∵$\sqrt{{a}_{1}}$=λa1+c,$\sqrt{{a}_{1}+{a}_{2}}=λ{a}_{2}$+c,
$\sqrt{{a}_{1}+{a}_{2}+{a}_{3}}$=λa3+c,
∴$\sqrt{{a}_{1}+{a}_{2}}$-$\sqrt{{a}_{1}}$=λd,
$\sqrt{{a}_{1}+{a}_{2}+{a}_{3}}$-$\sqrt{{a}_{1}}$=2λd,
∴a1+a2=${a}_{1}+{λ}^{2}{d}^{2}$+$2λd\sqrt{{a}_{1}}$,化为a2=λ2d2+$2λd\sqrt{{a}_{1}}$,
a1+a2+a3=a1+4λ2d2+$4λd\sqrt{{a}_{1}}$,化为a3=3λ2d2+$2λd\sqrt{{a}_{1}}$,
相减可得:2λ2d=1.
∴λ=$\sqrt{\frac{1}{2d}}$=$\frac{1}{\sqrt{2d}}$.
把$\sqrt{{a}_{1}}$=λa1+c代入a2=λ2d2+$2λd\sqrt{{a}_{1}}$,
可得:a1+d=λ2d2+2λd(λa1+c),
化为:λc=$\frac{1}{4}$,
∴c=$\frac{\sqrt{2d}}{4}$,λa1=c,∴a1=$\frac{d}{2}$.
∴$\sqrt{{S}_{n}}$=$\frac{1}{\sqrt{2d}}{a}_{n}$+$\frac{\sqrt{2d}}{4}$,
∴Sn=$\frac{1}{2d}{a}_{n}^{2}$+$\frac{1}{2}{a}_{n}$+$\frac{1}{8}d$.
∴n≥2时,an=Sn-Sn-1=$\frac{1}{2d}{a}_{n}^{2}$+$\frac{1}{2}{a}_{n}$+$\frac{1}{8}d$-$(\frac{1}{2d}{a}_{n-1}^{2}+\frac{1}{2}{a}_{n-1}+\frac{1}{8}d)$,
化为:(an+an-1)(an-an-1-d)=0,
∵an+an-1>0,
∴an-an-1=d=常数,a1=$\frac{d}{2}$.
∴{an}为等差数列.
点评 本题考查了数列的递推关系、等差数列的都用及其通项公式、方程的解法、数学归纳法,考查了变形能力、推理能力与计算能力,属于难题.

| A. | $\left\{{x|\frac{1}{2}<x<1}\right\}$ | B. | $\left\{{x|\frac{1}{2}≤x<1}\right\}$ | C. | $\left\{{x|\frac{1}{3}<x<\frac{1}{2}}\right\}$ | D. | ∅ |
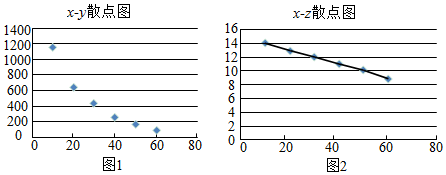
| 利润x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| Z=2ln(y) | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
(Ⅰ)根据散点图判断,y与x、z与x哪一对具有较强线性相关性?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字)
(Ⅲ)利润为多少元/kg时,年利润的预报值最大?
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…(xn,yn),其回归直线$\overline{y}$=$\stackrel{∧}{a}$+
$\stackrel{∧}{b}$$\overline{x}$的斜率和截距的最小二乘估计分别为:$\widehatb=\frac{{\sum_{i=1}^{i=n}{({{x_i}-\overline x})•({{y_i}-\overline y})}}}{{\sum_{i=1}^{i=n}{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^{i=n}{{x_i}•{y_i}-n•\overline x\overline{•y}}}}{{\sum_{i=1}^{i=n}{{x_i}^2-n•{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb•\overline x$
 某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.
某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.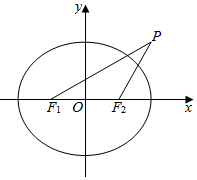 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.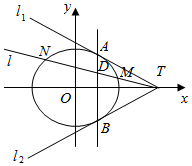 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.