题目内容
(12分)已知函数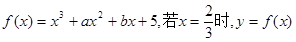 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3.
(1)求函数 的解析式;
的解析式;
(2)求 在
在 上的最大值和最小值.
上的最大值和最小值.
(1)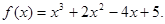 (2)在[-4, 1]上的最大值为13,最小值为-11。
(2)在[-4, 1]上的最大值为13,最小值为-11。
解析试题分析:(1)先求函数f(x)=x3+ax2+bx+5的导函数,再由x=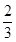 时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值
时,y=f(x)有极值,列一方程,曲线y=f(x)在点f(1)处的切线斜率为3,列一方程,联立两方程即可得a、b值
(2)先求函数f(x)=x3+ax2+bx+5的导函数,再解不等式得函数的单调区间,最后列表列出端点值f(-4),f(1)及极值,通过比较求出y=f(x)在[-4,1]上的最大值和最小值。
解:(1)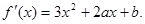
由题意,得
所以,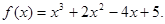
(2)由(1)知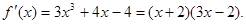 ,
,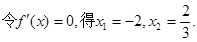

-4 (-4,-2) -2 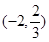
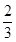

1 
+ 0 - 0 + 


极大值 

极小值 

函数值  练习册系列答案
练习册系列答案
世超金典基本功测评试卷系列答案
七鸣巅峰对决系列答案
天天练习王口算题卡口算速算巧算系列答案
育才课堂教学案系列答案
新课标教材同步导练绩优学案系列答案
智慧鸟单元评估卷系列答案
中考必备河南中考试题精选精析卷系列答案
小学英语测试AB卷系列答案
学法大视野单元测试卷系列答案
新领程必考口算应用题系列答案
相关题目


 ,
, 的值;
的值; 的最小值。
的最小值。 )
)
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。 ,曲线
,曲线 过点
过点 ,且在点
,且在点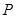 处的切线斜率为2.
处的切线斜率为2.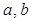 的值;
的值;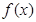 的极值点;
的极值点;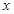 ,不等式
,不等式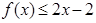 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。

 时,不等式
时,不等式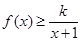 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围; .
.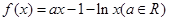 .
.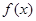 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对 恒成立,求实数
恒成立,求实数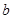 的取值范围.
的取值范围.  .
.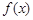 的单调性;
的单调性;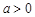 ,证明:当
,证明:当 时,
时,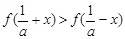 ;
; 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: (x0)<0.(本题满分14分)
(x0)<0.(本题满分14分)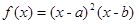 (
(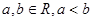 ).
).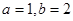 时,求曲线
时,求曲线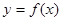 在点
在点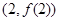 处的切线方程;
处的切线方程; 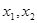 是
是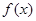 的两个极值点,
的两个极值点,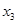 是
是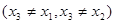 .证明:存在实数
.证明:存在实数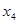 ,使得
,使得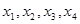 按某种顺序排列后构成等差数列,并求
按某种顺序排列后构成等差数列,并求 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,讨论
时,讨论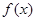 的单调性.
的单调性. .
.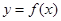 在点
在点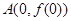 处的切线方程;
处的切线方程; 时,求函数
时,求函数 的单调区间.
的单调区间.