题目内容
2.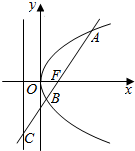 如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{BF}{BC}$=$\frac{\sqrt{5}}{5}$,则|AB|=5.
如图,直线l过抛物线y2=4x的焦点F且分别交抛物线及其准线于A,B,C,若$\frac{BF}{BC}$=$\frac{\sqrt{5}}{5}$,则|AB|=5.
分析 作AM、BN垂直准线于点M、N,根据$\frac{BF}{BC}$=$\frac{\sqrt{5}}{5}$,和抛物线的定义,可得tan∠NCB=2,从而可得直线方程,与抛物线方程联立,利用抛物线的定义,即可得出结论.
解答 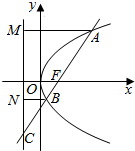 解:设A(x1,y1),B(x2,y2),
解:设A(x1,y1),B(x2,y2),
作AM、BN垂直准线于点M、N,则|BN|=|BF|,
∵$\frac{BF}{BC}$=$\frac{\sqrt{5}}{5}$,∴sin∠NCB=$\frac{\sqrt{5}}{5}$,
∴tan∠NCB=2
∴AF的方程为y=2(x-1),
代入y2=4x,可得x2-3x+1=0
∴x1+x2=3,
∴|AB|=x1+x2+2=5.
故答案为:5.
点评 此题是个中档题.考查抛物线的定义,考查学生分析解决问题的能力,属于中档题..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.设p:x<1,q:-1<x<1,则p是q成立的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
17.定义域为R的偶函数f(x)满足对?x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(|x|+1)至少有6个零点,则a的取值范围是( )
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{\sqrt{3}}{3}$) | C. | (0,$\frac{\sqrt{5}}{5}$) | D. | (0,$\frac{\sqrt{6}}{6}$) |
11.(1)记函数φ(x)=ax2-2x+1+ln(x+1)的图象为C,l为曲线C在点P(0,1)的切线,若存在a≥$\frac{1}{2}$,使直线l与曲线C有且仅有一个公共点,求满足条件的所有a的值;
(2)判断xsinx=1(x∈(0,5))实根的个数;
(3)完成填空
(2)判断xsinx=1(x∈(0,5))实根的个数;
(3)完成填空
| 用方程表述 | 用函数零点表述 | |
| 若函数y=f(x)和y=g(x)的图象在(a,b)内有交点 |