题目内容
已知向量i=(1,0),j=(0,1),a=i-2j,b=i+λj,且a与b的夹角为锐角,则实数λ的取值范围( )
A.(-∞,-2)∪(-2, ) ) | B.(-∞,  ) ) |
C.(-2, ) ) | D.(-∞,-2) |
A
解析试题分析:根据题意向量i=(1,0),j=(0,1),a=i-2j,b=i+λj,且a与b的夹角为锐角,则可知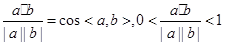 ,则首先考虑为
,则首先考虑为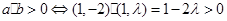 ,同时两个向量不能共线且同向,则可知
,同时两个向量不能共线且同向,则可知 ,故可知参数的范围为选A.
,故可知参数的范围为选A.
考点:向量的夹角公式运用
点评:解决该试题的关键是对于向量的数量积公式的变形,以及向量夹角的理解和准确运用,易错点就是对于夹角为锐角,则认为只要数量积为正数即可,就是漏情况的解法。

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
平面向量 ,
, ,若
,若 与
与 共线,则
共线,则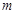 的值为( )
的值为( )
A.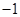 | B.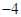 | C.1 | D.4 |
平面向量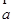 与
与 的夹角为
的夹角为 ,
, ,则
,则 =( )
=( )
A. | B.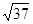 | C.7 | D.3 |
已知向量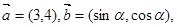 且
且 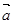 //
//  ,则
,则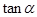 =( )
=( )
A.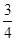 | B.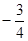 | C.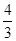 | D.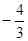 |
已知平面向量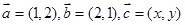 ,且满足
,且满足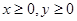 。若
。若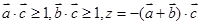 ,则 ( )
,则 ( )
A. 有最大值-2 有最大值-2 | B.z有最小值-2 | C.z有最大值-3 | D.z有最小值-3 |
已知 为坐标原点,
为坐标原点,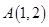 ,点
,点 的坐标
的坐标 满足约束条件
满足约束条件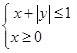 ,则
,则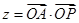 的最大值为
的最大值为
A. | B.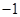 | C.1 | D.2 |
已知 三点不共线,对平面
三点不共线,对平面 外的任一点
外的任一点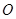 ,下列条件中能确定点
,下列条件中能确定点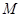 与点
与点 一定共面的是
一定共面的是 ( )
( )
A.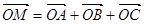 |
B. |
C.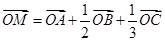 |
D. |
已知平面向量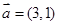 ,
,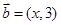 ,且
,且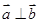 ,则实数
,则实数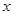 的值为
的值为
A.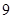 | B. | C.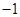 | D.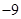 |
设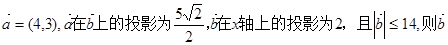 为( )
为( )
| A.(2,14) | B. | C.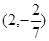 | D.(2,8) |