题目内容
已知平面向量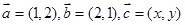 ,且满足
,且满足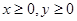 。若
。若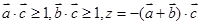 ,则 ( )
,则 ( )
A. 有最大值-2 有最大值-2 | B.z有最小值-2 | C.z有最大值-3 | D.z有最小值-3 |
A
解析试题分析:因为 ,所以
,所以 ,画出线性约束条件的可行域,目标函数
,画出线性约束条件的可行域,目标函数 ,由可行域可知z有最大值-2.
,由可行域可知z有最大值-2.
考点:平面向量的数量积;简单的线性规划问题。
点评:措辞提的关键是,能转化为线性规划的有关问题。考查了学生分析问题可转化问题的能力。求目标函数的最值,通常要把目标函数 转化为斜截式的形式,即
转化为斜截式的形式,即 的形式,但要注意
的形式,但要注意 的正负。当
的正负。当 为正时,求z的最大值就是求直线
为正时,求z的最大值就是求直线 在y轴上的截距最大时对应的点;当
在y轴上的截距最大时对应的点;当 为负时,求z的最大值就是求直线
为负时,求z的最大值就是求直线 在y轴上的截距最小时对应的点。
在y轴上的截距最小时对应的点。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知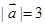 ,
, 在
在 方向上的投影为
方向上的投影为 ,则
,则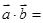
| A.3 | B.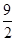 | C.2 | D.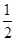 |
已知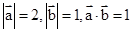 ,,则向量
,,则向量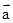 在
在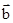 方向上的投影是( )
方向上的投影是( )
A.- | B.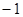 | C. | D.1 |
已知 ,
, ,
, ,
, ,则
,则 的最大值为( )
的最大值为( )
A. | B. 2 | C. | D. |
已知向量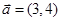 ,
, 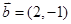 ,如果向量
,如果向量 与
与 垂直,则
垂直,则 的值为( )
的值为( )
A.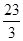 | B.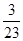 | C.2 | D.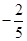 |
已知向量i=(1,0),j=(0,1),a=i-2j,b=i+λj,且a与b的夹角为锐角,则实数λ的取值范围( )
A.(-∞,-2)∪(-2, ) ) | B.(-∞,  ) ) |
C.(-2, ) ) | D.(-∞,-2) |
如图:在平行四边形 中,
中, 与
与 交于点
交于点
 ,设
,设
 = ( )
= ( )
A. | B. |
C.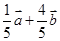 | D. |
 、
、 、
、 ,且满足
,且满足 ,|
,|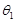 ,
,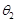 ,
, ,则它们的大小关系是( )
,则它们的大小关系是( )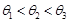


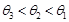
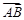 |=a,|
|=a,|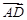 |=b,则
|=b,则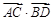 =
=