题目内容
设x1,x2∈R,常数a>0,定义运算“*”:x1*x2=(x1+x2)2-(x1-x2)2.(1)若x≥0,求动点P(x,![]() )轨迹C的方程;
)轨迹C的方程;
(2)若a=2,不过原点的直线l与x轴,y轴的交点分别为T,S,并且与(1)中轨迹C交于不同的两点P,Q,试求![]() +
+![]() 的取值范围;
的取值范围;
(3)设P(x,y)是平面上的任一点,定义d1(P)=![]()
![]() ,d2(P)=
,d2(P)=![]()
![]() .若在(1)中轨迹C上存在不同的两点A1,A2,使得d1(Ai)=
.若在(1)中轨迹C上存在不同的两点A1,A2,使得d1(Ai)=![]() d2(Ai)(i=1,2)成立,求实数a的取值范围.
d2(Ai)(i=1,2)成立,求实数a的取值范围.
解:(1)设y=![]() .
.
又由y=![]() ≥0,可得动点P(x,
≥0,可得动点P(x,![]() )轨迹C的方程为y2=4ax(y≥0).
)轨迹C的方程为y2=4ax(y≥0).
(2)由题得y2=8x(y≥0),设直线l:x=my+c,依题意m>0,c<0,则T(c,0).S,T,P,Q都在直线l上,
则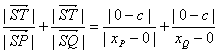 =|c|(
=|c|(![]() ).
).
由题得c<0,xP>0,xQ>0,
∴ =-c·(
=-c·(![]() )=
)=![]() .
.
由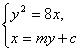 消去y得x2-(2c+8m2)x+c2=0.
消去y得x2-(2c+8m2)x+c2=0.
∴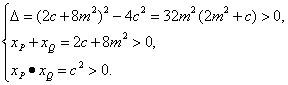
∵c<0,∴m2>![]() c,代入xP+xQ=2c+8m2,xP·xQ=c2,得
c,代入xP+xQ=2c+8m2,xP·xQ=c2,得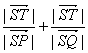 =2
=2![]() ,
,
又由m2>![]() c,c<0知
c,c<0知![]() <
<![]() ,
,
∴![]() >4,-2
>4,-2![]() >2,
>2,
即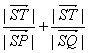 的取值范围是(2,+∞).
的取值范围是(2,+∞).
(3)由d1(P)=![]() =
=![]() ,
,
d2(P)=![]() =|x-a|,
=|x-a|,
设A1(x1,y1),A2(x2,y2),依题意则有![]() |x1-a|,
|x1-a|,![]() |x2-a|,
|x2-a|,
故方程![]() |x-a|在x∈[0,+∞)上有两个不等的实数解.
|x-a|在x∈[0,+∞)上有两个不等的实数解.
平方整理有(a-1)x2-(2a2+4a)x+a3=0在x∈[0,+∞)上有两个不等的实数解.
∴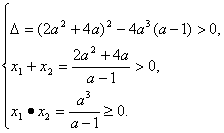 又因a>0,得a>1.故实数a的取值范围是(1,+∞).
又因a>0,得a>1.故实数a的取值范围是(1,+∞).

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
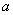 >0,定义运算“*”,x1*x2=(xl+x2)2-(x1-x2)2,若≥0,则动点
>0,定义运算“*”,x1*x2=(xl+x2)2-(x1-x2)2,若≥0,则动点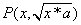 的轨迹是 ( )
的轨迹是 ( )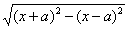 的取值范围.
的取值范围.