题目内容
如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2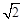 ,则EF的长为( )
,则EF的长为( )

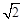 ,则EF的长为( )
,则EF的长为( )
A.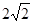 | B.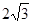 | C.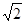 | D.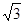 |
C
分析:Rt△CBP中,由勾股定理求得⊙P的半径BP,再由直角三角形CBP和CEF相似,对应边成比例得
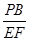 =
= 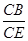 ,求出EF的长.
,求出EF的长.解:设⊙P 的半径为 r,Rt△CBP中,由勾股定理得 8+r2=(2+r)2,
∴r=1. 由Rt△CBP和R t△CEF相似可得
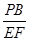 =
= 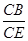 ,即
,即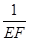 =
=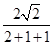 ,
,∴EF=
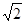 .
.故答案为:C.

练习册系列答案
相关题目
 以
以 为圆心,
为圆心, 为半径,过点
为半径,过点 作直线
作直线 与圆
与圆
 求直线
求直线 时,过直线
时,过直线 作圆
作圆 为切点
为切点 使
使 求点
求点 的坐标;
的坐标; 的中点为
的中点为 试在平面上找
试在平面上找 一点
一点 ,使
,使
 的长为定值.
的长为定值.
 (
( 为参数)与
为参数)与 轴的交点,且与直线
轴的交点,且与直线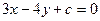 相切的圆C的极坐标方程是
相切的圆C的极坐标方程是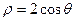 ,则
,则 。
。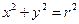 ,定点
,定点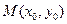 ,直线
,直线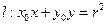 有如下两组论断:
有如下两组论断:
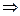 q的形式) ▲ .
q的形式) ▲ . 选一题做答,如果多做,则按所做的第一题记分。
选一题做答,如果多做,则按所做的第一题记分。 如图,
如图, 内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且
内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且


 ,⊙O的半径为1,
,⊙O的半径为1, 为弧
为弧 的中点,求
的中点,求 的长。
的长。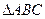 中,
中,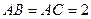 ,分别以
,分别以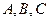 为圆心,以
为圆心,以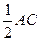 为半径做弧,则三条弧与边
为半径做弧,则三条弧与边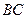 围成的图形(图中阴影部分)的面积为 .
围成的图形(图中阴影部分)的面积为 .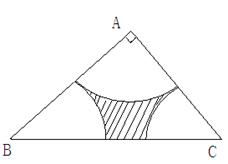
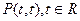 ,点
,点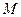 是圆
是圆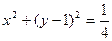 上的动点,点
上的动点,点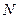 是圆
是圆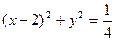
 的最大值是
的最大值是