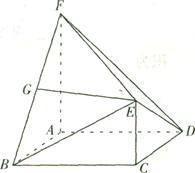
题目内容
在正三棱 ( )
( )
 ( )
( )A. | B. | C. | D. |
B
试题分析:根据题意,由于正三棱柱
 中,在底面ABC的下方补上一个同样的三棱柱,使得
中,在底面ABC的下方补上一个同样的三棱柱,使得 平移到下面的三棱柱的对角线,这样可以使得
平移到下面的三棱柱的对角线,这样可以使得 相交,利用解三角形的知识来求解异面直线所成的角,根据题意,由于设
相交,利用解三角形的知识来求解异面直线所成的角,根据题意,由于设 ,那么可知得到的三角形是等腰三角形,且腰长为
,那么可知得到的三角形是等腰三角形,且腰长为 ,同时底边长为
,同时底边长为 ,则由余弦定理可知
,则由余弦定理可知
 ,则可知异面直线所成的角为直角,故选B.
,则可知异面直线所成的角为直角,故选B.点评:解决该试题的关键是将直线平移到一个三角形中,结合中位线定理来得到,属于基础题。

练习册系列答案
相关题目
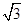 ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
 ,m
,m ,则
,则 ,
,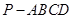 中,四边形
中,四边形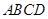 是菱形,
是菱形,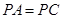 ,
,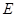 为
为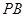 的中点.
的中点.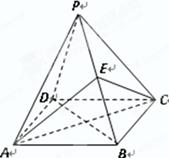
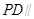 面
面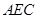 ; (2)求证:平面
; (2)求证:平面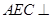 平面
平面 .
.
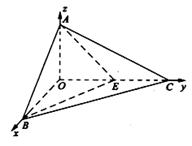
 中,E是BC的中点,F是
中,E是BC的中点,F是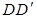 的中点
的中点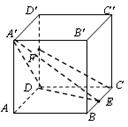
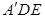
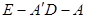 的平面角的余弦值.
的平面角的余弦值.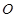 的面上有四点
的面上有四点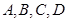 ,
,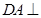 平面
平面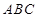 ,
,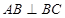 ,
,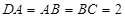 ,则球
,则球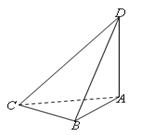
 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA