题目内容
若函数f(x)=(x2-2ax)ex在[-1,1]上为单调函数,求实数a的取值范围.
解:∵x∈R,f'(x)=ex[x2+2(1-a)x-2a]
1)若f(x)在[-1,1]递减,则f'(x)≤0在[-1,1]恒成立,
∴只需x2+2(1-a)x-2a≤0在[-1,1]恒成立,
即2a(x+1)≥x2+2x在[-1,1]恒成立,
(1)x=-1时(1)式成立;x∈(-1,1]时,需满足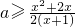 ,令g(x)=
,令g(x)=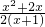 ,
,
则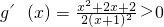 在x∈(-1,1]恒成立,
在x∈(-1,1]恒成立,
∴g(x)在(-1,1]递增,∴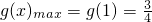 ,∴
,∴ ;
;
2)若f(x)在[-1,1]递增,则f'(x)≥0在[-1,1]恒成立,
但f'(-1)=-1,∴f(x)在[-1,1]不递增;
综上 .
.
分析:先由f′(x)>0,再根据函数f(x)在[-1,1]上为单调函数,将原问题转化为x2+2(1-a)x-2a≤0在[-1,1]恒成立问题,列出关于a的不等关系解之即得.
点评:本小题主要考查函数单调性的应用、利用导数研究函数的单调性、不等式的解法等基础知识,考查运算求解能力,属于基础题.
1)若f(x)在[-1,1]递减,则f'(x)≤0在[-1,1]恒成立,
∴只需x2+2(1-a)x-2a≤0在[-1,1]恒成立,
即2a(x+1)≥x2+2x在[-1,1]恒成立,
(1)x=-1时(1)式成立;x∈(-1,1]时,需满足
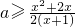 ,令g(x)=
,令g(x)=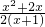 ,
,则
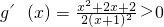 在x∈(-1,1]恒成立,
在x∈(-1,1]恒成立,∴g(x)在(-1,1]递增,∴
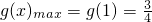 ,∴
,∴ ;
;2)若f(x)在[-1,1]递增,则f'(x)≥0在[-1,1]恒成立,
但f'(-1)=-1,∴f(x)在[-1,1]不递增;
综上
 .
.分析:先由f′(x)>0,再根据函数f(x)在[-1,1]上为单调函数,将原问题转化为x2+2(1-a)x-2a≤0在[-1,1]恒成立问题,列出关于a的不等关系解之即得.
点评:本小题主要考查函数单调性的应用、利用导数研究函数的单调性、不等式的解法等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
若函数 f(x)=a x (a>0,a≠1 ) 的部分对应值如表:
| x | -2 | 0 |
| f(x) | 0.592 | 1 |
则不等 式f-1(│x│<0)的解集是 ()
A. {x│-1<x<1} B. {x│x<-1或x>1}
C. {x│0<x<1} D. {x│-1<x<0或0<x<1}
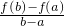 (x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中:
(x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中: ;
; 级线性逼近”的函数的个数为
级线性逼近”的函数的个数为 (x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中:
(x-a)|≤T(T为常数)成立,则称函数f(x)在[a,b]上具有“T级线性逼近”.下列函数中: ;
; 级线性逼近”的函数的个数为( )
级线性逼近”的函数的个数为( )