题目内容
若sinx-
cosx=4a+6,则a的取值范围是( )
| 3 |
分析:先利用两角和公式对函数解析式化简整理,再根据正弦函数的特点求出sinx-
cosx的值域,进而得出a取值范围.
| 3 |
解答:解:∵sinx-
cosx=2sin(x-
)
∴-2≤sinx-
cosx=4a+6≤2
解得:-2≤a≤-1
故选:B.
| 3 |
| π |
| 6 |
∴-2≤sinx-
| 3 |
解得:-2≤a≤-1
故选:B.
点评:本题主要考查了利用两角和公式的化简三角函数以及最值,熟练掌握公式是解题的关键,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
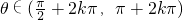 (k∈Z),求角α的各三角函数值.
(k∈Z),求角α的各三角函数值. ,且0<x<π,求tanx的值.
,且0<x<π,求tanx的值. (k∈Z),求角α的各三角函数值.
(k∈Z),求角α的各三角函数值. ,且0<x<π,求tanx的值.
,且0<x<π,求tanx的值.