题目内容
8.函数y=x2+2x+3的奇偶性为非奇非偶函数.分析 根据函数奇偶性的定义进行判断即可.
解答 解:∵y=x2+2x+3,
∴对称轴为x=-1,
则对称轴不是y轴,
故函数y=x2+2x+3为非奇非偶函数,
故答案为:非奇非偶函数
点评 本题主要考查函数奇偶性的判断,利用一元二次函数的对称性是解决本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
19.已知函数f(x)=2sin(π-x)•cosx-2sin2x+1,若f($\frac{{x}_{0}}{2}$)=$\frac{\sqrt{3}}{3}$,x0∈(-$\frac{π}{4}$,$\frac{π}{4}$),则cos2x0等于( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{3}}{9}$ |
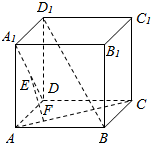 如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.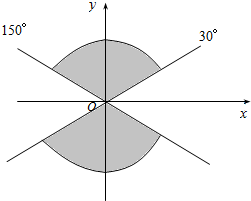 已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.
已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.