题目内容
平面上三个力F1,F2,F3作用于一点且处于平衡状态,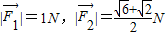 ,
, ,
,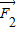 的夹角为45°,则
的夹角为45°,则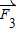 与
与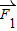 的夹角为( )
的夹角为( )A.30°
B.150°
C.15°
D.135°
【答案】分析:三个力平衡则三个力的和为  ;移项,利用向量模的平方等于向量的平方求出则
;移项,利用向量模的平方等于向量的平方求出则 的模,利用三角函数的余弦定理求出两个向量的夹角大小.
的模,利用三角函数的余弦定理求出两个向量的夹角大小.
解答:解:∵三个力平衡,∴ ,(2分)
,(2分)
∴| |=|
|=| |=
|=
= =
= =
= +1,(6分)
+1,(6分)
而 与
与  的夹角可由余弦定理求得,
的夹角可由余弦定理求得,
cos< >=
>= =
= ,
,
∴ 与
与  的夹角为30°(10分)
的夹角为30°(10分)
则F3与F1的夹角为180°-30°=150°.(12分)
点评:本题考查向量模的性质:向量模的平方等于向量的平方、考查三角形的余弦定理.
 ;移项,利用向量模的平方等于向量的平方求出则
;移项,利用向量模的平方等于向量的平方求出则 的模,利用三角函数的余弦定理求出两个向量的夹角大小.
的模,利用三角函数的余弦定理求出两个向量的夹角大小.解答:解:∵三个力平衡,∴
 ,(2分)
,(2分)∴|
 |=|
|=| |=
|=
=
 =
= =
= +1,(6分)
+1,(6分)而
 与
与  的夹角可由余弦定理求得,
的夹角可由余弦定理求得,cos<
 >=
>= =
= ,
,∴
 与
与  的夹角为30°(10分)
的夹角为30°(10分)则F3与F1的夹角为180°-30°=150°.(12分)
点评:本题考查向量模的性质:向量模的平方等于向量的平方、考查三角形的余弦定理.

练习册系列答案
相关题目
平面上三个力F1,F2,F3作用于一点且处于平衡状态,|
|=1N,|
|=
N,
,
的夹角为45°,则
与
的夹角为( )
| F1 |
| F2 |
| ||||
| 2 |
| F1 |
| F2 |
| F3 |
| F1 |
| A、30° | B、150° |
| C、15° | D、135° |