题目内容
(满分14分)已知函数

(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,讨论
时,讨论 的单调性.
的单调性.


(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)当
 时,讨论
时,讨论 的单调性.
的单调性.(1)
(2)当 时,
时, 在
在 上单调递减,在
上单调递减,在 单调递增;
单调递增;
当 时
时 ,
, 在
在 上单调递减;
上单调递减;
当 时,
时, 在
在 和
和 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。

(2)当
 时,
时, 在
在 上单调递减,在
上单调递减,在 单调递增;
单调递增;当
 时
时 ,
, 在
在 上单调递减;
上单调递减;当
 时,
时, 在
在 和
和 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。解:(1)当 时,
时, ,则
,则 ,又
,又 ,则曲线
,则曲线 在点
在点 处的切线斜率为
处的切线斜率为 ,因此,切线方
,因此,切线方 程为
程为 ,即
,即
(2) ,设
,设 ,
, ,则
,则 符号相同。
符号相同。
 ①若
①若 ,
, ,
,
当 时,
时, 上单调递增;
上单调递增;
当 时,
时, 上单调递减。
上单调递减。
②若 ,则
,则 ,即
,即 ,解得
,解得 。
。
当 时,
时, ,
, 恒成立,即
恒成立,即 恒成立,因此
恒成立,因此 在
在 上单调递减;
上单调递减;
当 时,
时, 。可列表如下:
。可列表如下:
综上所述:当 时,
时, 在
在 上单调递减,在
上单调递减,在 单调递增;
单调递增;
当 时
时 ,
, 在
在 上单调递减;
上单调递减;
当 时,
时, 在
在 和
和 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
 时,
时, ,则
,则 ,又
,又 ,则曲线
,则曲线 在点
在点 处的切线斜率为
处的切线斜率为 ,因此,切线方
,因此,切线方 程为
程为 ,即
,即
(2)
 ,设
,设 ,
, ,则
,则 符号相同。
符号相同。 ①若
①若 ,
, ,
,当
 时,
时, 上单调递增;
上单调递增;当
 时,
时, 上单调递减。
上单调递减。②若
 ,则
,则 ,即
,即 ,解得
,解得 。
。当
 时,
时, ,
, 恒成立,即
恒成立,即 恒成立,因此
恒成立,因此 在
在 上单调递减;
上单调递减;当
 时,
时, 。可列表如下:
。可列表如下: |  |  |  |
 (与 (与 符号一致) 符号一致) |  |  |  |
 |  |  |  |
 时,
时, 在
在 上单调递减,在
上单调递减,在 单调递增;
单调递增;当
 时
时 ,
, 在
在 上单调递减;
上单调递减;当
 时,
时, 在
在 和
和 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
练习册系列答案
相关题目
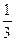
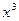 +
+ 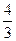 .
.
 处的切线的方程;
处的切线的方程;
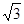
 ,若
,若 ,则
,则 ( )
( )



 ,过点
,过点 作曲线
作曲线 的切线,则此切线方程为
的切线,则此切线方程为  对于任意实数
对于任意实数 满足条件
满足条件 ,若
,若 则
则 _______.
_______. 在
在
 处的切线斜率为
处的切线斜率为 ,则
,则 = .
= .
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,讨论
时,讨论 的单调性.
的单调性.