题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,且atanB=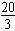 ,bsinA=4。
,bsinA=4。
(1)求cosB和a;
(2)若△ABC的面积S=10,求cos4C的值。
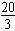 ,bsinA=4。
,bsinA=4。(1)求cosB和a;
(2)若△ABC的面积S=10,求cos4C的值。
解:(1)由bsinA=4,得asinB=4,
又atanB=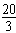 ,
,
∴cosB=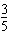
又由atanB=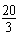 ,知tanB>0,
,知tanB>0,
则sinB=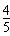 ,tanB=
,tanB=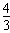 ,故a=5。
,故a=5。
(2)由S=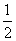 acsinB,得c=5,
acsinB,得c=5,
∴A=C
由cos4C=2cos22C-1=2cos2(A+C)-1=2cos2B-1
=2×(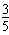 )2-1=-
)2-1=-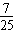 。
。
又atanB=
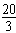 ,
,∴cosB=
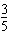
又由atanB=
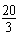 ,知tanB>0,
,知tanB>0,则sinB=
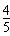 ,tanB=
,tanB=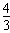 ,故a=5。
,故a=5。(2)由S=
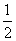 acsinB,得c=5,
acsinB,得c=5,∴A=C
由cos4C=2cos22C-1=2cos2(A+C)-1=2cos2B-1
=2×(
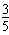 )2-1=-
)2-1=-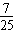 。
。
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目