题目内容
已知圆A:(x+3)2+y2=100,圆A内一定点B(3,0),动圆P过B点且与圆A内切,求圆心P的轨迹方程.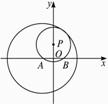
解:设|PB|=r.
∵圆P与圆A内切,圆A的半径为10,
∴两圆的圆心距|PA|=10-r,
即|PA|+|PB|=10(大于|AB|).
∴点P的轨迹是以A,B两点为焦点的椭圆.
∴2a=10,2c=|AB|=6.
∴a=5,c=3.
∴b2=a2-c2=25-9=16,
即点P的轨迹方程为![]() .
.
点评:(1)本例的解法抓住了两圆内切的特点,得出|PA|+|PB|=10,所以点P的轨迹方程是以A、B为焦点的椭圆的标准方程,这就把求点P的轨迹方程的问题转化成了求A2、B2的问题.(2)转化题中的条件,利用定义判断出点的轨迹,再根据轨迹方程特征(类似于公式)用待定系数法求出常数,简便快捷.在条件转化过程中,要充分利用其几何性质.

练习册系列答案
相关题目