题目内容
有红、蓝、黄三种颜色的球各3个,每种颜色的3个球分别标有数字1、2、3,将此9个球排成3行3列,要求同行颜色相同,但同列中任何两个数字不相同,则不同的排法有 种.
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:完成此任务需分四步,第一步确定三行颜色,第二步确定第一行球号,第三步确定第二行球号,注意此步受前一步影响,最后一步已确定,最后各步计数结果相乘即可
解答:
解:第一步,排列三行的颜色,共有
=6种排法;
第二步,为第一行的3个球排序,共有
=6种排法;
第三步,为第二行的3个球排序,共有2种排法;
第四步,为第三行的3个球排序,共有1种排法;
故不同的排法共有6×6×2×1=72种
故答案为:72.
| A | 3 3 |
第二步,为第一行的3个球排序,共有
| A | 3 3 |
第三步,为第二行的3个球排序,共有2种排法;
第四步,为第三行的3个球排序,共有1种排法;
故不同的排法共有6×6×2×1=72种
故答案为:72.
点评:本题主要考查了计数的方法和技巧,分步计数原理及其应用,排列数组合数公式的运用,恰当分步,准确计数是解决本题的关键,属基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目

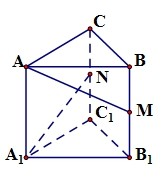 13、如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,若M,N分别是BB1,CC1的中点,则异面直线AM与A1N所成的角的大小为
13、如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,若M,N分别是BB1,CC1的中点,则异面直线AM与A1N所成的角的大小为