题目内容
在△ABC中,角A,B,C所对的边分别为a、b、c,若a、b是方程x2-2
x+2=0的两根,且cosAcosB-sinAsinB=
;
(1)求角C的大小;
(2)求边c的长度;
(3)求△ABC的面积.
| 3 |
| 1 |
| 2 |
(1)求角C的大小;
(2)求边c的长度;
(3)求△ABC的面积.
考点:余弦定理,两角和与差的余弦函数,正弦定理
专题:解三角形
分析:(1)已知等式左边利用两角和与差的余弦函数公式化简求出A+B的值,进而确定出C的值;
(2)由a、b是方程x2-2
x+2=0的两根,利用韦达定理表示出a+b与ab,利用余弦定理列出关系式,再利用完全平方公式变形后,将a+b与ab的值代入计算即可求出c的值;
(3)由ab及sinC的值,利用三角形面积公式即可求出三角形ABC面积.
(2)由a、b是方程x2-2
| 3 |
(3)由ab及sinC的值,利用三角形面积公式即可求出三角形ABC面积.
解答:
解:(1)∵cosAcosB-sinAsinB=cos(A+B)=
,
∵A+B∈(0,π),
∴A+B=
,
∴C=
;
(2)∵a、b是方程x2-2
x+2=0的两根,
∴a+b=2
,ab=2,
∴由余弦定理得:c2=a2+b2-2abcosC=a2+b2+ab=(a+b)2-ab=10,
则c=
;
(3)∵ab=2,sinC=
,
∴S△ABC=
absinC=
×2×
=
.
| 1 |
| 2 |
∵A+B∈(0,π),
∴A+B=
| π |
| 3 |
∴C=
| 2π |
| 3 |
(2)∵a、b是方程x2-2
| 3 |
∴a+b=2
| 3 |
∴由余弦定理得:c2=a2+b2-2abcosC=a2+b2+ab=(a+b)2-ab=10,
则c=
| 10 |
(3)∵ab=2,sinC=
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:此题考查了余弦定理,三角形面积公式,以及两角和与差的余弦函数公式,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
定义
=a1a4-a2a3,若f(x)=
,则f(x)的图象向右平移
个单位得到的函数解析式为( )
|
|
| π |
| 3 |
A、y=2sin(x-
| ||
B、y=2sin(x+
| ||
| C、y=2cosx | ||
| D、y=2sinx |
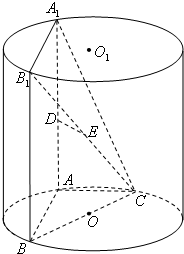 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.