题目内容
【题目】已知函数![]() .
.
(Ⅰ)探究函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)答案见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)对函数求导有![]() ,分类讨论:若
,分类讨论:若![]() ,
, ![]() 在
在![]() 上单调递增;若
上单调递增;若![]() ,
, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)原问题即![]() 在
在![]() 上恒成立.构造函数:令
上恒成立.构造函数:令![]() ,则
,则![]() ,考查分子部分,令
,考查分子部分,令![]()
![]() ,则
,则![]() 是
是![]() 上的增函数.据此分类讨论:①当
上的增函数.据此分类讨论:①当![]() 时,
时, ![]() 成立.②当
成立.②当![]() 时,
时, ![]() 不可能恒成立.综合上述,实数
不可能恒成立.综合上述,实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)依题意, ![]() ,函数
,函数![]() ,
,
若![]() ,
, ![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)依题意, ![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]()
![]() ,
,
令![]()
![]() ,则
,则![]() 是
是![]() 上的增函数,即
上的增函数,即![]() .
.
①当![]() 时,
时, ![]() ,所以
,所以![]() ,因此
,因此![]() 是
是![]() 上的增函数,
上的增函数,
则![]() ,因此
,因此![]() 时,
时, ![]() 成立.
成立.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
求得![]() ,(由于
,(由于![]() ,所以舍去
,所以舍去![]() )
)
当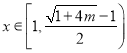 时,
时, ![]() ,则
,则![]() 在
在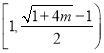 上递减,
上递减,
当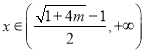 时,
时, ![]() ,则
,则![]() 在
在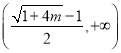 上递增,
上递增,
所以当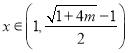 时,
时, ![]() ,
,
因此![]() 时,
时, ![]() 不可能恒成立.
不可能恒成立.
综合上述,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目