题目内容
（Ⅰ）用向量法证明：cos（α-β）=cosαcosβ+sinαsinβ．
（Ⅱ）若tan（α+β）=
，tan（α-
）=
，求：tan(β+
)的值．
（Ⅱ）若tan（α+β）=
| 2 |
| 5 |
| π |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
分析：（Ⅰ）建立直角坐标系，设的顶点在原点，始边在x轴非负半轴，角α、β的终边分别与单位圆交于M（cosα，sinα）、N（cosβ，sinβ），则由两个向量的数量积的定义可得
•
=cos(α-β)，再利用两个向量的数量积公式可得
•
=cosαcosβ+sinαsinβ，从而证得公式成立．
（Ⅱ）根据 tan(β+
)=tan[(α+β)-(α-
)]，再把已知条件代入运算求得结果．
| OM |
| ON |
| OM |
| ON |
（Ⅱ）根据 tan(β+
| π |
| 4 |
| π |
| 4 |
解答：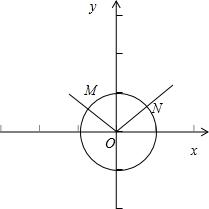
（Ⅰ）证明：建立直角坐标系，设的顶点在原点，始边在x轴非负半轴，
角α、β的终边分别与单位圆交于p1（cosα，sinα）、p2（cosβ，sinβ），
则由两个向量的数量积的定义可得
•
=|
||
|cos(α-β)=cos(α-β)，
再利用两个向量的数量积公式可得
•
=cosαcosβ+sinαsinβ，
∴cos（α-β）=cosαcosβ+sinαsinβ．
（Ⅱ） tan(β+
)=tan[(α+β)-(α-
)]=
=
．
（Ⅰ）证明：建立直角坐标系，设的顶点在原点，始边在x轴非负半轴，角α、β的终边分别与单位圆交于p1（cosα，sinα）、p2（cosβ，sinβ），
则由两个向量的数量积的定义可得
| OM |
| oON |
| OM |
| ON |
再利用两个向量的数量积公式可得
| OM |
| ON |
∴cos（α-β）=cosαcosβ+sinαsinβ．
（Ⅱ） tan(β+
| π |
| 4 |
| π |
| 4 |
| ||||
1+
|
| 3 |
| 22 |
点评：本题主要考查两个向量的数量积的定义、两个向量的数量积公式、两角差的正切公式，属于中档题．
练习册系列答案
相关题目
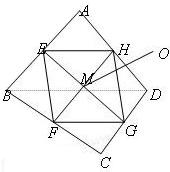已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点．
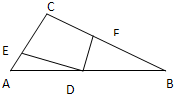（1）如图，D是Rt△ABC的斜边AB上的中点，E和F分别在边AC和BC上，且ED⊥FD，求证：EF2=AE2+BF2（EF2表示线段EF长度的平方）（尝试用向量法证明）
=
（
）.