题目内容
已知函数 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数.
(1)如果函数 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值;
的值;
(2)证明:函数 (常数
(常数 )在
)在 上是减函数;
上是减函数;
(3)设常数 ,求函数
,求函数 的最小值和最大值.
的最小值和最大值.
【答案】
解. (1) b=4.
(2) 证明略
(3) 当1<c≤3时, 函数f(x)的最大值是f(3)=3+ ;
;
当3<c<9时, 函数f(x)的最大值是f(1)=1+c.
【解析】本题考查函数的性质和应用,解题要认真审题,仔细求解
(1)根据题设条件知  =4,由此可知b=4.
=4,由此可知b=4.
(2)根据已知函数定义法,设出变量作差,变形定号,确定结论。
(3)根据∵c∈(1,9)然后得到函数的单调区间进而得到最值

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值。
的值。 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值; 有如下性质:如果常数
有如下性质:如果常数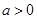 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值;
的值;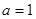 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在 上是减函数。
上是减函数。 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值;