题目内容
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2)
=1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2) 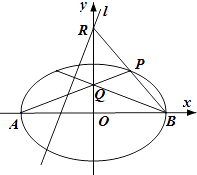
(1)求椭圆C的标准方程;
(2)求证: ![]() 为定值;
为定值;
(3)求证:过点R且与直线QB垂直的直线经过定点,并求出该定点的坐标.
【答案】
(1)解:由题意可得A(﹣a,0),B(a,0),
当点Q坐标为(0,1)时,点R坐标为(0,2),
即有kPA= ![]() ,直线PA:y=
,直线PA:y= ![]() x+1,
x+1,
kPB=﹣ ![]() ,直线PA:y=﹣
,直线PA:y=﹣ ![]() x+2,
x+2,
解得交点P( ![]() ,
, ![]() ),
),
代入椭圆方程可得 ![]() +
+ ![]() =1,
=1,
解得a= ![]() ,
,
则椭圆C的标准方程为 ![]() =1
=1
(2)证明:设Q(0,s),R(0,t),
由椭圆的方程可得A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),
,0),
即有直线PA:y= ![]() x+s,直线PB的方程为y=﹣
x+s,直线PB的方程为y=﹣ ![]() x+t,
x+t,
解得交点P( ![]() ,
, ![]() ),
),
代入椭圆方程可得 ![]() +
+ ![]() =1,
=1,
化简可得st=2,
即有 ![]() =st=2为定值;
=st=2为定值;
(3)证明:由(2)可得st=2,即t= ![]() ,
,
直线QB的斜率为k=﹣ ![]() ,
,
即有过点R且与直线QB垂直的直线方程为y= ![]() x+t,
x+t,
即为y= ![]() ,令x=﹣
,令x=﹣ ![]() ,可得y=0,
,可得y=0,
则过点R且与直线QB垂直的直线经过定点,坐标为(﹣ ![]() ,0)
,0)
【解析】(1)求得A,B的坐标,直线PA,PB的方程,求交点P,代入椭圆方程,解方程,可得a,进而得到椭圆方程;(2)设Q(0,s),R(0,t),求得直线PA,PB的方程,求交点P,代入椭圆方程,化简整理可得st=2,再由向量的数量积的坐标表示可得定值;(3)求得QB的斜率,运用两直线垂直的条件:斜率之积为﹣1,求得垂线的方程,由st=2,代入,结合直线恒过定点的求法,可得定点.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案